11.4.3 Distances

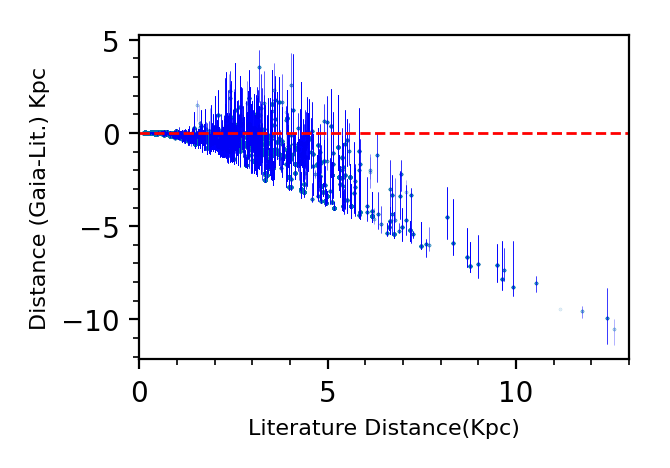
For single stars, GSP-Phot provides reliable distances out to $\sim$2kpc. Beyond this limit, GSP-Phot can systematically underestimate distance depending on the fractional parallax uncertainty, ${\sigma }_{\varpi }/\varpi$. In Figure 11.77, we compare the distances from GSP-Phot with literature values for each cluster analysed in Cantat-Gaudin et al. (2020). This catalogue used the Gaia DR2 data and a maximum likelihood approach, but we updated their results on parallaxes for the DR3 zero point. We emphasize that our comparison does not depend on Gaia DR2 systematics on astrometry. We obtain similar results when comparing GSP-Phot distances with those derived from color-magnitude diagram fitting by Kharchenko et al. (2013) and BOCCE (Bragaglia and Tosi 2006; Cantat-Gaudin et al. 2018).

However, when the fractional parallax uncertainties are small (about or $\varpi /{\sigma }_{\varpi }>5$), the distances from GSP-Phot remain overall reliable up to 10 kpc (see Figure 11.78). Yet, Figure 11.78b-d shows that the distributions of GSP-Phot distances and inverse parallaxes can be markedly different, depending on the parallax quality. We emphasize that the large discrepancy between GSP-Phot distances and the inverse parallaxes in Figure 11.78b is not fully explained by “inverting a noisy parallax measurement”. There is a real systematic underestimation of GSP-Phot distances that is most likely due to the GSP-Phot distance prior. When the parallax measurements are of sufficiently high quality (small uncertainties), the prior has little to no effects, which restores the agreement between the distances and parallaxes as shown in Figure 11.78d.

To investigate that the GSP-Phot distance prior is too harsh, we have reprocessed $5$ million sources with two additional different priors definitions. The distance estimates published in Gaia DR3, used an exponential distance prior with a scale length of 1/10 of the one derived from the mock catalogue of Rybizki et al. (2020) (see Section 11.3.3). In one reprocessing, we restored the actual length scale from the mock catalogue of Rybizki et al. (2020) (i.e., increased the Gaia DR3 one by a factor of 10.). In another reprocessing, we remove all priors, i.e., uniform up to 10 kpc. Figure 11.79 shows the resulting distance distributions. A weaker prior would have made GSP-Phot distances more consistent with the parallaxes, thereby confirming that the root cause of the distance bias issue. However, Figure 11.79 also shows that a the uniform prior is also non-optimal.

We compared GSP-Phot distances with those from asteroseismic analysis in Figure 11.80. Overall, we find a good agreement out to 2–3 kpc for both main-sequence and giant stars. Beyond this limit, we find more outliers and observe a systematic underestimation of distance, particularly for lower SNR on the parallax.

We combined the spectroscopic binaries from Pourbaix et al. (2004) and Traven et al. (2020b) to obtain a reference sample to investigate the quality of MSC’s distances. On this sample, we find that the distances from MSC are largely consistent with the parallaxes (see Figure 11.81a). Surprisingly though, Figure 11.81b shows that for these known binaries GSP-Phot distances that assume single stars agree better with the Gaia parallaxes than the MSC distances. We suspect that the spectroscopic binaries in Pourbaix et al. (2004) and Traven et al. (2020b) are so bright that their excellent parallaxes (small uncertainties) override the single-star assumption by GSP-Phot. MSC does not use the parallaxes in the same manner as GSP-Phot. A sample of fainter spectroscopic binaries should ideally show that MSC distances agree better with parallaxes than GSP-Phot distances.