3 Astrometry 3 Astrometry 3.2 Properties of the input data

3.1 Introduction

Author(s): David Hobbs

This chapter presents the models and processing steps used for Gaia’s core solution, namely, the Astrometric Global Iterative Solution (AGIS). The inputs to this solution rely heavily on the basic observables (or astrometric elementaries) which have been pre-processed and discussed in Chapter 2, the results of which will be published in Fabricius et al. (2016). The models consist of reference systems and time scales; assumed linear stellar motion and relativistic light deflection; in addition to fundamental constants and the transformation of coordinate systems. Higher level inputs such as: planetary and solar system ephemeris; Gaia tracking and orbit information; initial quasar catalogues and BAM data are all needed for the processing described here. The astrometric calibration models are outlined followed by the details processing steps which give AGIS its name. The final Section 3.5 represents a basic quality assessment and validation of the scientific results which will also be published in detail in Lindegren et al. (2016). However, the validation of the science products was not restricted to just this, a more independent catalogue consolidation and validation of the science results for Gaia DR1 was also performed and are documented in Chapter 7 and will be published in Arenou et al. (2017).

3.1.1 Overview

Author(s): Lennart Lindegren

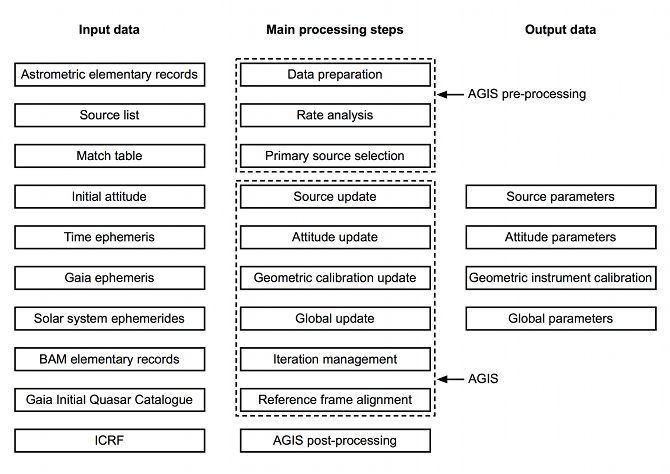
Figure 3.1: Overview of the main steps of the astrometric processing, and of its main input and output data.

The astrometric processing, as envisaged and designed before the launch of Gaia, is described in some detail in Lindegren et al. (2012). This reference is still very relevant, but confrontation with real data and a continuing maturing of concepts have resulted in many changes, and this chapter provides an updated description.

A schematic overview of the astrometric processing is given in Figure 3.1. The main objective of the astrometric processing is to estimate, as accurately as reasonably possible, a set of parameters representing the sources, the attitude, and the geometric calibration of the instrument. Optionally, a set of global parameters may also be estimated. These are the output data in Figure 3.1.

This objective is achieved by means of a complex processing chain applied to the input data represented in the left part of the figure and further described below. The core part of the processing is the Astrometric Global Iterative Solution (AGIS), which performs a weighted least-squares fit of the global astrometric model to the CCD observations by iteratively adjusting the output parameters.

The astrometric processing uses a coordinate system known as the Barycentric Coordinate Reference System (BCRS; Section 3.1.3). It has its origin at the solar-system barycentre (typically within two solar radii of the sun’s position). Its axes are non-rotating with respect to objects at cosmological distances and coincide with those of the International Celestial Reference Frame (ICRS; Arias et al. 1995). The time coordinate of the BCRS is the barycentric coordinate time (TCB).

The main input data are:

Figure 3.2: Reference systems and transformations for the global astrometric model.

The global astrometric model, which is fitted to the observations and that uses the source, attitude, calibration, and global parameters as unknowns, can be described as a succession of coordinate transformations, as depicted in Figure 3.2. The relevant coordinate systems are:

1.

The Barycentric Coordinate Reference System (BCRS) already introduced above. The astrometric parameters of the sources and the ephemerides use this reference system, with TCB as the time argument.
2.

The Centre-of-Mass Reference System (CoMRS) has its origin at the centre of mass of Gaia, and is co-moving with the satellite, but its axes are still non-rotating and aligned with the ICRS. The observed direction of a source in this reference system is obtained by a complex transformation of the source parameters, which is carried out in a general-relativistic framework by means of the Gaia Relativity Model (GREM; Section 3.1.5).
3.

The Scanning Reference System (SRS) is fixed with respect to the optics of the Gaia telescopes and thus rotates with the satellite at an angular velocity of about 60 ${}^{\prime\prime}$ s ${}^{-1}$ . The transformation between CoMRS and SRS is a pure spatial rotation, that is the attitude (Section 3.3.4).
4.

The CCD pixel coordinates are used to represent the elementary observations that are input to the astrometric processing (AstroElementaries). The along-scan coordinate is given by the observation time $t_{\text{obs}}$ , which is the precise time at which the optical image of a source passes an imaginary ‘observation line’ on the CCD. The across-scan coordinate $\mu$ is the mean pixel column index of the image during the CCD observation. $t_{\text{obs}}$ is obtained in OBMT essentially by counting TDI periods, and interpolating to a fraction of a TDI period. It can be transformed to TCB by means of the time ephemeris. Additional data associated with the CCD observation include the field-of-view index (preceding or following), the CCD index, and parameters defining the pixel window used to sample the observation. The transformation between the SRS and the CCD pixel coordinates is given by the geometric instrument model (Section 3.3.5), which describes the geometry of the CCD observation lines in the SRS.

The transformations described above do not explicitly involve the global parameters. Indeed, it is possible to do the astrometric processing without any global parameters. In contrast to the source, attitude, and calibration parameters, which represent very specific models, the global parameters can be used to model arbitrary effects influencing the observations as a function of time, source parameters, etc. This is achieved by means of the generic model described in Section 3.3.6. The global parameters could thus describe effects as diverse as a deviation of the post-Newtonian parameter $\gamma$ from unity, systematic velocity errors in the Gaia ephemeris, or periodic variations of the differential optical field distortion.

The main processing steps, as shown in Figure 3.1, are:

3.1.2 Conventions, notations, nomenclature, and definitions

Author(s): Uli Bastian

The Gaia data processing, like any other complex multi-partner project, needs a set of agreed conventions and notations to be followed by all partners. Such conventions are needed to ease communication, to avoid misunderstandings and to streamline the distributed development of software for shared usage.

The DPAC consortium maintains a set of internal documents intending to collect all the necessary conventions. However, it is neither needed nor useful to expose the users of the Gaia Catalogue(s) to the full set of conventions. Instead, it is better to restrict the documentation to those which are actually of interest to the external users. Also, it is not useful to concentrate their description in one place. Rather they should be introduced where needed.

So, for instance, the definitions and notations for angular coordinates, time scales and epochs, as well as relativistic reference frames are given in the following subsections where they first appear. The agreed fundamental physical and mathematical constants are briefly described in Section 3.1.8.

The present subsection mentions only a few overarching aspects.

Physical units: The SI system

This section is mainly based on the ‘Units home page’ of the National Institute of Standards and Technology (see the NIST website), which generally agrees with IAU recommendations For interested users we recommend to read Thompson and Taylor (2008). In summary, The Gaia collaboration uses ‘acceptable SI units’ (as defined below) as default, plus a few extensions also described below. Following Thompson and Taylor (2008), we interpret the term ‘SI units’ as the seven SI base units (kg, m, s, mol, A, K, cd; see Section 4.1 in Thompson and Taylor (2008)), plus the 20 SI derived units (N, V, Hz, Gy, W, etc.; see Section 4.2 in Thompson and Taylor (2008)), plus the two SI supplementary units (rad and sr; Section 4.2.2 in Thompson and Taylor (2008)), including multiples and sub-multiples of these units formed by using SI prefixes ( ${\rm M}=10^{6}$ , ${\rm k}=10^{3}$ , $\mu=10^{-6}$ , etc.; Table 5 in Thompson and Taylor (2008)). The term ‘acceptable SI units’ is taken to denote the ‘SI units’ (as defined above), plus those units accepted by the CIPM (Comité International des Poids et Mesures) for use with the SI (notably angular degree, arcminute, arcsecond, minute, hour, and day; Tables 6 and 7 in Thompson and Taylor (2008)), plus those units temporarily accepted for use with the SI (Table 9 and Section 5.2 in Thompson and Taylor (2008)), including multiples and sub-multiples of these units. We also follow Thompson and Taylor (2008) and the IAU by recognizing that the use of time intervals expressed in units of Julian years (year), distances in units of parsecs (pc) or astronomical units (au), and source brightness/luminosity in units of magnitudes (mag) is allowed. The use of the non-SI unit Å is ‘temporarily accepted’ by Thompson and Taylor (2008) and ‘deprecated’ by the IAU; we propose that this unit is not used.

Notation of units

The interested reader is strongly advised to consult Thompson and Taylor (2008); we simply list a few specific remarks which are relevant in the light of Gaia:

•

The angular units degree, arcminute, arcsecond may be abbreviated as ‘deg’, ‘arcmin’, ‘arcsec’ or denoted by the conventional symbols ${}^{\circ}~{}^{\prime}~{}^{\prime\prime}$ .
•

Sub-multiples of the arcsecond are denoted by ‘mas’ ( $10^{-3}$ arcseconds, 1 milli-arcsecond) and ‘ $\mu$ as’ ( $10^{-6}$ arcseconds, 1 micro-arcsecond). In an ASCII-environment ‘ $\mu$ as’ is allowed to degenerate into ‘muas’.
•

The unit of a Julian year is denoted as ‘year’, in line with Thompson and Taylor (2008), §5.1.1. In theory, some confusion could arise when using ‘y’ instead of ‘year’. For instance the SI unit ‘Gy’ (Gray, for absorbed radiation dose) could be mis-interpreted as $10^{9}$ years. To add to this confusion, we note that the (‘temporarily accepted’) radiation unit ‘rad’ (not to be confused with radian) is defined as ‘cGy’, i.e., centi-Gray. Although in the light of Gaia, this sort of confusion is generally not expected, the unit ‘year’ should either be spelt out explicitly, or be abbreviated solely by ‘a’ (from Latin ‘annum’, following ISO and Section 8.1 of Thompson and Taylor (2008).
•

The use of the phrase/unit ‘micron’ to denote $\mu$ m is not allowed; this unit should be denoted as ‘ $\mu$ m’ (or as ‘micrometer’ in full or ‘mum’ in abbreviation in an ASCII-environment).
•

Note the distinction between a bit (b) and a byte (B, meaning eight bits). Thus: 1 kb denotes one kilobit ( $10^{3}$ bit) and 1 kB denotes one kilobyte ( $10^{3}$ byte).
•

Note the distinction between binary and decimal prefixes. For example, one kilobit (kb) denotes $10^{3}=1000$ bit but one kibibit (Kib) denotes $2^{10}=1024$ bit. The prefix kilobinary, or kibi or Ki, means $2^{10}$ . More examples of binary prefixes, e.g. Mi= $2^{20}\sim 10^{6}$ , Gi= $2^{30}\sim 10^{9}$ and a complete list can be found here.

Acronyms

A very special set of conventions is a list of about 3000 acronyms and abbreviations used in the Gaia collaboration. It is maintained in the internal “Glossary of acronyms”. The list of acronyms and abbreviations attached to this documentation of the Gaia Data Release is a tailored excerpt of that glossary.

3.1.3 Reference systems and time scales

Author(s): Sergei Klioner

Gaia data processing is based on the rigorous relativistic definitions of reference systems including time scales as their integral parts. All reference systems are defined in the framework of General Relativity theory by their respective metric tensors that can be found in the literature. A set of rigorous 4-dimensional relativistic transformations ensures correct use of various coordinates and time scale as needed.

The primary reference system used in the data modelling is the Barycentric Celestial Reference System (BCRS; Soffel et al. 2003). The BCRS has its origin at the solar-system barycentre and its axes are aligned with the ICRS. The time-like coordinate of the BCRS is TCB. The motions of Gaia and other solar-system objects are thus described in terms of the space-like coordinates of the BCRS, $x^{i}(t)$ , using TCB as the independent time variable $t$ . In particular, Gaia makes use of the TCB-based solar system ephemeris INPOP10e (see Section 3.2.1). The motions of all objects beyond the solar-system are also parametrized in terms of BCRS coordinates, but here the independent time variable $t$ should be understood as the time at which the event would be observed at the solar-system barycentre, i.e. the time of observation corrected for the Rømer delay (Klioner 2003, Sect.8). This convention is necessitated by the in general poor knowledge of distances beyond the solar-system. The resulting astrometric catalogue is also parametrized by TCB.

The Centre-of-Mass Reference System (CoMRS; Klioner 2004) is a physically adequate local (proper) reference system for the Gaia spacecraft. The origin coincides with the centre of mass of the Gaia satellite. The CoMRS is chosen to be kinematically non-rotating, that is, it is related to the BCRS by the generalized Lorentz transformation without spatial rotation. The coordinate basis of the CoMRS at its origin coincides with a particular form of tetrad co-moving with the observer. This means that the CoMRS description of observables coincides with the classical tetrad representation in cases where a tetrad is sufficient for modelling. However, the CoMRS is a complete rigorously-defined 4-dimensional reference system suitable to describe local physical processes localized in the body of Gaia satellite. Its coordinate time at the origin coincides with the proper time of Gaia — the reading of ideal clock co-moving with the satellite. The CoMRS gives a relativistic definition of the Gaia attitude that is defined as a Euclidean spatial rotation in the CoMRS coordinates. The CoMRS is also used in the relativistic model of observations as well as in the model for the calibration of Gaia’s on-board clock.

The Geocentric Celestial Reference System (GCRS; Soffel et al. 2003) is only used in Gaia for processing of auxiliary time transfer data (time couples, see Section 3.1.6). In particular, the GCRS is used to compute the BCRS position of the ESA ground stations at particular moments of time. The time scales related to GCRS (TCG, TT, etc.) are also only used in the intermediate calculations related to the calibration of Gaia’s clock.

3.1.4 Standard model of stellar motion

Author(s): Lennart Lindegren

In the astrometric processing described in this chapter, the motions in the BCRS of all sources beyond the solar-system (i.e., stars and extragalactic objects) are modelled using the ‘standard model of stellar motion’. This model was also used in the construction of the Hipparcos Catalogue (ESA 1997, Volume 1, Section 1.2.8). The model assumes that the source is moving with uniform velocity relative to the solar-system barycentre (SSB), and its barycentric position $\boldsymbol{b}(t)$ is thus described by the linear model

\boldsymbol{b}(t)=\boldsymbol{b}_{\text{ep}}+(t-t_{\text{ep}})\boldsymbol{v}

(3.1)

with six parameters, namely the components in BCRS of $\boldsymbol{b}_{\text{ep}}$ (unit: m) and $\boldsymbol{v}$ (unit: m s ${}^{-1}$ ). $t_{\text{ep}}$ is the reference epoch of the catalogue. The barycentric coordinate direction (unit vector) to the source at time $t$ (in TCB) is then

\boldsymbol{\bar{u}}_{\text{B}}(t)=\left\langle\boldsymbol{b}_{\text{ep}}+(t-t% _{\text{ep}})\boldsymbol{v}\right\rangle\,,

(3.2)

where the angular brackets signify vector normalisation: $\langle\boldsymbol{a}\rangle=\boldsymbol{a}|\boldsymbol{a}|^{-1}$ . Equation 3.2 ignores the finite speed of light. In principle, the barycentric coordinate direction measured at time $t$ corresponds to the barycentric position of the source at the time $t-|\boldsymbol{b}|c^{-1}$ , several (or many) years earlier. However, it would be highly impractical to take this into account because the distance $|\boldsymbol{b}|$ is rarely known to sufficient accuracy. The standard model is therefore parametrised by quantities representing the position and motion of the source as they appear from the SSB at a given time. Thus, the time argument in $\boldsymbol{\bar{u}}_{\text{B}}(t)$ must always be interpreted as the time of light arrival at the SSB, not as the time of light emission from the source.

For similar reasons it would be highly impractical to use the rectangular components of $\boldsymbol{b}_{\text{ep}}$ and $\boldsymbol{v}$ as the parameters of the standard model. By convention, the six parameters of the standard model are instead defined as follows (Klioner 2003; Lindegren et al. 2012):

•

The barycentric right ascension $\alpha$ and declination $\delta$ at the reference epoch are defined in terms of the barycentric coordinate direction at the reference epoch, expressed in the BCRS as

$\boldsymbol{\bar{u}}_{\text{B}}(t_{\text{ep}})=\begin{bmatrix}\cos\alpha\cos% \delta\\ \sin\alpha\cos\delta\\ \sin\delta\end{bmatrix}\,.$ (3.3)
•

The components of the proper motion in right ascension $\mu_{\alpha*}$ and in declination $\mu_{\delta}$ at the reference epoch are defined in terms of the derivatives of the barycentric coordinate direction at the reference epoch, expressed in the BCRS as

$\left.\frac{\text{d}\boldsymbol{\bar{u}}_{\text{B}}}{\text{d}t}\right|_{t=t_{% \text{ep}}}=\begin{bmatrix}-\sin\alpha\\ \cos\alpha\\ 0\end{bmatrix}\mu_{\alpha*}+\begin{bmatrix}-\cos\alpha\sin\delta\\ -\sin\alpha\sin\delta\\ \cos\delta\end{bmatrix}\mu_{\delta}\,.$ (3.4)
•

The parallax $\varpi$ is related to the barycentric distance to the source according to

$\varpi=|\boldsymbol{b}|\,A_{\text{u}}^{-1}\,,$ (3.5)

where $A_{\text{u}}=149\,597\,870\,700$ m is the astronomical unit (Capitaine 2012).
•

The sixth parameter quantifies the radial motion of the source relative to the SSB, and may be taken to be the radial velocity $v_{r}$ (more precisely the astrometric radial velocity; see Lindegren and Dravins 2003), or alternatively the ‘radial proper motion’

$\mu_{r}=v_{r}\varpi A_{\text{u}}^{-1}\,.$ (3.6)

As can be seen by comparing Equation 3.5 and Equation 3.6 the radial proper motion is the relative change in distance per unit time, and can be expressed in the same unit as the transverse proper motion components $\mu_{\alpha*}$ and $\mu_{\delta}$ .

(The notations $\boldsymbol{r}$ , $\boldsymbol{p}$ , and $\boldsymbol{q}$ are later introduced for the three unit vectors appearing in Equation 3.3 and Equation 3.4.)

Although there are thus six astrometric parameters that could be fitted to the observations according to the standard model, the radial velocity is always taken from spectroscopic measurements (ground-based catalogues or Gaia’s Radial Velocity Spectrometer). Therefore, only $\alpha$ , $\delta$ , $\varpi$ , $\mu_{\alpha*}$ , and $\mu_{\delta}$ are in practise fitted to the data; they are commonly referred to as the ‘five astrometric parameters’. Nevertheless, for applying the model, and propagating the parameters between epochs, all six parameters are needed. $\mu_{r}=0$ is assumed if the radial velocity is not known.

The conventional unit for $\alpha$ and $\delta$ is degrees or radians, for $\varpi$ it is mas, and for $\mu_{\alpha*}$ , $\mu_{\delta}$ , and $\mu_{r}$ it is mas per Julian year of 31 557 600 s TCB, abbreviated mas yr ${}^{-1}$ . Differential quantities in $\alpha$ and $\delta$ ( $\Delta\alpha*\equiv\Delta\alpha\cos\delta$ and $\Delta\delta$ ), including uncertainties, are expressed in mas.

That the standard model of stellar motions neglects light-time effects has some non-trivial consequences (Stumpff 1985; Butkevich and Lindegren 2014). Apart from the obvious fact that the currently measured directions to the stars represent their actual positions in space at a much earlier epoch, we need to consider the following.

1.

For the modelling of the apparent motions of stars in our Galaxy, the standard model is always adequate at the precision of Gaia, in the sense that the neglected light-time effects at most produce prediction errors in position of $\sim$ 10 $\mu$ as after a ten-year interval, and much smaller errors for most stars over much longer intervals of time.
2.

For the interpretation of the astrometric parameters in terms of the physical motion of stars in the Galaxy, it may be necessary to take light-time effects into account for a wider range of objects. The dominant effect is that the Doppler factor, equal to $(1-v_{r}/c)^{-1}$ , where $c$ is the speed of light, needs to be included when calculating the (true) space velocity of a star from its (apparent) astrometric parameters (cf. Klioner 2003).

These two effects should not be confused with the far more important perspective acceleration (e.g., van de Kamp 1981), which is a purely geometrical effect caused by the changing distance to the source and changing angle between the velocity vector and the line of sight. It is an observationally well-established effect that needs to be taken into account in the astrometric solutions for all high-velocity, nearby stars (cf. de Bruijne and Eilers 2012). The perspective acceleration is fully accounted for in the standard model, provided that the radial velocity is known and used in the model.

While the standard model is routinely fitted to all non-solar-system sources observed by Gaia, it will give a bad fit for a substantial fraction of the sources that have manifestly non-uniform space motions or other complications. These include astrometric binaries and exoplanetary systems, resolved or partially resolved non-single stars with significant orbital motion, variability-induced movers (VIMs), stars with surface structure, and various kinds of extended objects. The Gaia observations of such sources are analysed in the special DPAC ‘Object Processing’, using a range of dedicated procedures. It is however important that the standard model is fitted also to these sources, as it provides in most cases a meaningful approximation to the astrometric parameters, and since the goodness-of-fit can be used to select sources for the object processing.

The standard model is also used for quasars and other sufficiently point-like extragalactic objects. Their parallaxes and proper motions are fitted exactly as for stars, even though it is known a priori that they are very small. This is important in order not to force (i.e. bias) the solution and because the classification of the source could be wrong; but also because the fitted parameters are needed for aligning the reference frame of Gaia (Section 3.3.2) and in the quality assessment (Section 3.5.10).

3.1.5 Relativistic model

Author(s): Sergei Klioner

Section 3.1.3 gives an overview of the set of relativistic reference systems used in Gaia data processing. The Barycentric Celestial Reference System (BCRS) is used to model the motion of celestial bodies both inside and outside the solar-system. From the relativistic point of view, the Gaia catalogue is the model of Universe expressed in the BCRS. All astrometric parameters — parallaxes (distances), proper motions, positions — are defined in the BCRS coordinates. The goal of the relativistic model — called Gaia Relativity Model (GREM) — is to compute (predict) the observed CoMRS direction towards a source given its parameters in BCRS. The details of the model can be found in Klioner (2003, 2004); Klioner and Peip (2003); Klioner and Zschocke (2010); Zschocke and Klioner (2011).

Using the standard model of stellar motion described in Section 3.1.4 the astrometric parameters of a source are used to compute the coordinate BCRS direction from the location of Gaia at the moment of observation to the source $\boldsymbol{\bar{u}}(t)$ . This direction has to be transformed into the observed direction $\boldsymbol{u}$ with respect to CoMRS.

The transformation essentially consists of two steps. First, the light propagation from the source to the location of Gaia is modelled in the BCRS in full details required to reach the required numerical accuracy of about 0.1 $\mu$ as. In this process, the influence of the gravitational field of the solar-system is taken into account. This includes the gravitational light-bending due to the Sun, the major planets and the Moon. More deflecting bodies are readily available and can be used for special purposes (e.g. special processing of the data close to Jupiter foreseen in the future). Both post-Newtonian and post-post-Newtonian effects are calculated. In this process special care was given to the relation between the analytical order of smallness of the effects and their numerical magnitude (Klioner and Zschocke 2010). In particular, only the so-called enhanced post-post-Newtonian effects, which can exceed 1 $\mu$ as in some special observational configurations, are taken into account.

For observations close to the giant planets the effects of their quadrupole gravitational fields are taken into account in the post-Newtonian approximation. The effective computation of the rather complicated quadrupole deflection of light represents a separate problem (Zschocke and Klioner 2011). To speed up the computations of the model, the post-Newtonian formula for the quadrupole deflection was simplified as much as possible to give the required numerical accuracy of at least 0.1 $\mu$ as for the realistic observational configuration in Gaia. Besides that, a very efficient criterion was found allowing one to decide if the actual calculation of the quadrupole deflection is needed. The criterion allows one to estimate the quadrupole deflection using only three multiplications.

The non-stationarity of the gravitational field (in particular, due to translational motion of the solar-system bodies) is also properly taken into account (Klioner 2003, 2003; Klioner and Peip 2003, and references therein).

No attempt is made to account for effects of the gravitational field outside the solar-system. This plays a role only in cases when its influence is variable on time scales comparable with the duration of observations, e.g. in various gravitational lensing phenomena.

The second step is to compute the observed direction $\boldsymbol{u}$ in CoMRS from the computed BCRS direction of light propagation at the location of Gaia at the moment of observation (Klioner (2003, Section 5) and Klioner (2004, Section VI)). Technically, the transformation represents a closed-form Lorentz transformation with the velocity of Gaia as seen by an fictitious observer that is co-located with Gaia at the moment of observation, but having zero BCRS velocity. One can show that that “observed” velocity $\boldsymbol{v}$ is the BCRS velocity of Gaia $\boldsymbol{v}_{\text{{Gaia}}}$ multiplied by a factor depending on the gravitational potential at the location of Gaia.

Besides astrometric parameters of the sources, GREM requires several kinds of auxiliary data:

–

Gaia spatial ephemeris (BCRS position and velocity of Gaia for any moment of time covered by observations; Section 3.2.3);
–

Gaia time ephemeris (the relation between the readings of the Gaia on-board clock and TCB; Section 3.1.6);
–

Solar-system ephemeris; the INPOP10e ephemeris (Fienga et al. 2016) parametrized by TCB is used in the Gaia data processing (see Section 3.2.1);
–

Various astronomical and physical constants; this includes the constants used in INPOP10e (masses of all major bodies of the solar-system, etc.).

3.1.6 Time scales

Author(s): Sergei Klioner

As explained in Section 3.1.3, Gaia data processing uses the rigorous relativistic definitions of reference systems including time scales as their integral parts. The coordinate time of BCRS — TCB (Soffel et al. 2003) — is used throughout data processing and parametrizes the final Gaia catalogue.

Another important technical time coordinate used in Gaia data processing is the On-Board Mission Timeline (OBMT). OBMT represents the readings of the on-board Gaia atomic clock plus a constant chosen for each continuous time interval between Gaia clock resets in such a way that OBMT remains increasing with physical time. Strictly speaking, OBMT is not a time scale since it is not necessarily continuous. OBMT is a purely technical time coordinate that is however unique for any event on board of Gaia. Although the raw observations of Gaia are parametrized by OBMT, for various purposes (e.g. interrogating the solar-system and Gaia ephemerides), OBMT should be related to TCB. This is done by creating the Gaia time ephemeris — a model of Gaia’s clock fitted to the special time synchronization data — the one-way time transfer from Gaia to the ESA ground stations (Klioner 2015).

3.1.7 Transformations of astrometric data and error propagation

Author(s): Lennart Lindegren

Only the transformation to galactic coordinates is covered here. Epoch transformation is covered by Section 4.3.2.

Galactic coordinates

The positions and proper motions of non-solar system objects derived from Gaia observations are expressed in the International Celestial Reference System (ICRS). This is an inertial (non-rotating) reference system, which since 1998 replaces the various earlier celestial reference frames (referred to by names such as FK5, FK4, J2000, B1950, equinox and equator of 1950.0, etc.).

For galactic research it is often desirable to use galactic coordinates instead of ICRS. Unfortunately there is no accurate transformation from ICRS to galactic coordinate sanctioned by the IAU. (The existing IAU resolution from 1958 defines the galactic axes with reference to the equatorial B1950 system, which cannot be accurately transformed to the ICRS; see Murray 1989.) We therefore adopt the same definition as was used in the Hipparcos Catalogue (Vol. 1, Sect. 1.5.3 of ESA 1997). According to this, the ICRS coordinates of the north galactic pole are $(\alpha_{\text{G}},\,\delta_{\text{G}})=(192.85948^{\circ},\,+27.12825^{\circ})$ and the galactic longitude of the first intersection of the galactic plane with the equator is $l_{\Omega}=32.93192^{\circ}$ .

Transformation of position

Transformation of astronomical spherical coordinates ( $\alpha$ , $\delta$ in ICRS; $l$ and $b$ in the galactic system) and of the corresponding proper motions ( $\mu_{\alpha*}$ , $\mu_{\delta}$ and $\mu_{l*}$ , $\mu_{b}$ , respectively) is best done by using vectors and matrix algebra (see Ch. 4 in van Altena 2012). A given point on the celestial sphere is then represented by a unit vector, whose components in the two systems are

\boldsymbol{r}_{\text{ICRS}}=\begin{bmatrix}X_{\text{ICRS}}\\ Y_{\text{ICRS}}\\ Z_{\text{ICRS}}\end{bmatrix}=\begin{bmatrix}\cos\alpha\cos\delta\\ \sin\alpha\cos\delta\\ \sin\delta\end{bmatrix}

(3.7)

and

\boldsymbol{r}_{\text{Gal}}=\begin{bmatrix}X_{\text{Gal}}\\ Y_{\text{Gal}}\\ Z_{\text{Gal}}\end{bmatrix}=\begin{bmatrix}\cos l\cos b\\ \sin l\cos b\\ \sin b\end{bmatrix}\,.

(3.8)

In terms of these column matrices the transformation from ICRS to the galactic system is obtained through the matrix multiplication

\boldsymbol{r}_{\text{Gal}}=\boldsymbol{A}_{\text{G}}^{\prime}\boldsymbol{r}_{% \text{ICRS}}\,,

(3.9)

where

	$\displaystyle\boldsymbol{A}_{\text{G}}^{\prime}$	$\displaystyle=\boldsymbol{R}_{z}(-l_{\Omega})\boldsymbol{R}_{x}(90^{\circ}-% \delta_{\text{G}})\boldsymbol{R}_{z}(\alpha_{\text{G}}+90^{\circ})$		(3.10)
		$\displaystyle=\begin{bmatrix}-0.0548755604162154&-0.8734370902348850&-0.483835% 0155487132\\ +0.4941094278755837&-0.4448296299600112&+0.7469822444972189\\ -0.8676661490190047&-0.1980763734312015&+0.4559837761750669\end{bmatrix}$		(3.11)

is a fixed orthogonal matrix (the transpose of the matrix $\boldsymbol{A}_{\text{G}}$ defined in Vol. 1, Eq. 1.5.11 of ESA 1997). $\boldsymbol{R}_{i}(\theta)$ is the $3\times 3$ matrix representing a rotation of the coordinate frame by the angle $\theta$ about axis $i$ . Since $\boldsymbol{A}_{\text{G}}^{\prime}$ is orthogonal, the inverse transformation to Equation 3.9 is

\boldsymbol{r}_{\text{ICRS}}=\boldsymbol{A}_{\text{G}}\boldsymbol{r}_{\text{% Gal}}\,.

(3.12)

Given $(\alpha,\,\delta)$ , application of Equation 3.7 and Equation 3.9 gives the galactic position in Cartesian coordinates. Some care should be exercised when converting the Cartesian coordinates to spherical ( $l$ , $b$ ) in order to avoid quadrant ambiguity and numerical inaccuracy near the poles. Recommended formulae (e.g. Ch. 4 in van Altena 2012) use the four-quadrant inverse tangent (atan2 or similar) available in all high-level programming languages:

l=\text{atan2}(Y_{\text{Gal}},\,X_{\text{Gal}})\,,\quad b=\text{atan2}\left(Z_% {\text{Gal}},\,\sqrt{X_{\text{Gal}}^{2}+Y_{\text{Gal}}^{2}}\right)\,.

(3.13)

Note that Equation 3.13 works also for vectors that are not of unit length.

Transformation of proper motion

The transformation of the proper motion components $(\mu_{\alpha*},\,\mu_{\delta})$ to $(\mu_{l*},\,\mu_{b})$ (where $\mu_{l*}=\mu_{l}\cos b$ ) requires the use of the four auxiliary column matrices

\boldsymbol{p}_{\text{ICRS}}=\begin{bmatrix}-\sin\alpha\\ \cos\alpha\\ 0\end{bmatrix}\,,\quad\boldsymbol{q}_{\text{ICRS}}=\begin{bmatrix}-\cos\alpha% \sin\delta\\ -\sin\alpha\sin\delta\\ \cos\delta\end{bmatrix}

(3.14)

and

\boldsymbol{p}_{\text{Gal}}=\begin{bmatrix}-\sin l\\ \cos l\\ 0\end{bmatrix}\,,\quad\boldsymbol{q}_{\text{Gal}}=\begin{bmatrix}-\cos l\sin b% \\ -\sin l\sin b\\ \cos b\end{bmatrix}\,.

(3.15)

Geometrically, $\boldsymbol{p}_{\text{ICRS}}$ and $\boldsymbol{q}_{\text{ICRS}}$ represent unit vectors in the directions of increasing $\alpha$ and $\delta$ , respectively, expressed by their Cartesian components in ICRS. Similarly, $\boldsymbol{p}_{\text{Gal}}$ and $\boldsymbol{q}_{\text{Gal}}$ are unit vectors in the directions of increasing $l$ and $b$ , respectively, expressed by their Cartesian components in the galactic system. The Cartesian components of the so-called proper motion vector can now be written in ICRS as

\boldsymbol{\mu}_{\text{ICRS}}=\boldsymbol{p}_{\text{ICRS}}\mu_{\alpha*}+% \boldsymbol{q}_{\text{ICRS}}\mu_{\delta}\,,

(3.16)

and in the galactic system as

\boldsymbol{\mu}_{\text{Gal}}=\boldsymbol{p}_{\text{Gal}}\mu_{l*}+\boldsymbol{% q}_{\text{Gal}}\mu_{b}\,.

(3.17)

These column matrices transform exactly as any other Cartesian vector, namely

\boldsymbol{\mu}_{\text{Gal}}=\boldsymbol{A}_{\text{G}}^{\prime}\boldsymbol{% \mu}_{\text{ICRS}}

(3.18)

and

\boldsymbol{\mu}_{\text{ICRS}}=\boldsymbol{A}_{\text{G}}\boldsymbol{\mu}_{% \text{Gal}}\,.

(3.19)

Applying Equation 3.14, Equation 3.16, and Equation 3.18 therefore gives the Cartesian proper motion vector in the galactic system, from which the components along $l$ are $b$ are obtained by means of Equation 3.17, using the orthogonality of $\boldsymbol{p}_{\text{Gal}}$ and $\boldsymbol{q}_{\text{Gal}}$ :

\mu_{l*}=\boldsymbol{p}_{\text{Gal}}^{\prime}\boldsymbol{\mu}_{\text{Gal}}\,,% \quad\mu_{b}=\boldsymbol{q}_{\text{Gal}}^{\prime}\boldsymbol{\mu}_{\text{Gal}}\,.

(3.20)

For completeness we give also the corresponding calculation in ICRS:

\mu_{\alpha*}=\boldsymbol{p}_{\text{ICRS}}^{\prime}\boldsymbol{\mu}_{\text{% ICRS}}\,,\quad\mu_{\delta}=\boldsymbol{q}_{\text{ICRS}}^{\prime}\boldsymbol{% \mu}_{\text{ICRS}}\,.

(3.21)

Error propagation

The statistical errors associated with the astrometric parameters $\alpha$ , $\delta$ , $\varpi$ , $\mu_{\alpha*}$ , and $\mu_{\delta}$ are given by the standard uncertainties $\sigma_{\alpha*}$ , $\sigma_{\delta}$ , $\sigma_{\varpi}$ , $\sigma_{\mu\alpha*}$ , and $\sigma_{\mu\delta}$ together with the correlation coefficients $\rho(\alpha,\delta)$ , $\rho(\alpha,\varpi)$ , etc. For notational convenience we may number the five parameters 0, 1, $\dots$ , 4; thus $\sigma_{0}=\sigma_{\alpha*}$ , $\rho_{01}=\rho(\alpha,\delta)$ , etc. Let

\boldsymbol{e}\equiv\begin{bmatrix}e_{0}\\ e_{1}\\ e_{2}\\ e_{3}\\ e_{4}\end{bmatrix}=\begin{bmatrix}\Delta\alpha*\\ \Delta\delta\\ \Delta\varpi\\ \Delta\mu_{\alpha*}\\ \Delta\mu_{\delta}\end{bmatrix}

(3.22)

be a vector containing the errors, that is the differences between the measured and true astrometric parameters, expressed in mas or mas yr ${}^{-1}$ (with $\Delta\alpha*=\Delta\alpha\cos\delta$ ). The measurements are assumed to be unbiased, so the expectation of the error vector is

\text{E}\left[\boldsymbol{e}\right]=\boldsymbol{0}

(3.23)

and its covariance is the symmetric positive definite matrix

\boldsymbol{C}=\text{E}\left[\boldsymbol{e}\boldsymbol{e}^{\prime}\right]=% \begin{bmatrix}\text{E}\left[e_{0}e_{0}\right]&\text{E}\left[e_{0}e_{1}\right]% &\cdots&\text{E}\left[e_{0}e_{4}\right]\\ \text{E}\left[e_{1}e_{0}\right]&\text{E}\left[e_{1}e_{1}\right]&\cdots&\text{E% }\left[e_{1}e_{4}\right]\\ \vdots&\vdots&\ddots&\vdots\\ \text{E}\left[e_{4}e_{0}\right]&\text{E}\left[e_{4}e_{1}\right]&\cdots&\text{E% }\left[e_{4}e_{4}\right]\end{bmatrix}

(3.24)

with diagonal elements $C_{ii}=\sigma_{i}^{2}$ and off-diagonal elements $V_{ij}=\sigma_{i}\sigma_{j}\rho_{ij}$ (with $\rho_{ji}=\rho_{ij}$ ).

The transformation from ICRF to galactic coordinates is a strongly non-linear function. However, the errors $e_{i}$ are very small and the error vector in galactic coordinates

\boldsymbol{g}\equiv\begin{bmatrix}g_{0}\\ g_{1}\\ g_{2}\\ g_{3}\\ g_{4}\end{bmatrix}=\begin{bmatrix}\Delta l*\\ \Delta b\\ \Delta\varpi\\ \Delta\mu_{l*}\\ \Delta\mu_{b}\end{bmatrix}

(3.25)

is therefore obtained by the linear transformation

\boldsymbol{g}=\boldsymbol{J}\boldsymbol{e}\,,

(3.26)

where

\boldsymbol{J}=\frac{\partial(l*,\,b,\,\varpi,\,\mu_{l*},\,\mu_{b})}{\partial(% \alpha*,\,\delta,\,\varpi,\,\mu_{\alpha*},\,\mu_{\delta})}=\begin{bmatrix}% \frac{\partial l*}{\partial\alpha*}&\frac{\partial l*}{\partial\delta}&\cdots&% \frac{\partial l*}{\partial\mu_{\delta}}\\ \frac{\partial b}{\partial\alpha*}&\frac{\partial b}{\partial\delta}&\cdots&% \frac{\partial b}{\partial\mu_{\delta}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial\mu_{b}}{\partial\alpha*}&\frac{\partial\mu_{b}}{\partial\delta}% &\cdots&\frac{\partial\mu_{b}}{\partial\mu_{\delta}}\end{bmatrix}

(3.27)

is the Jacobian of the transformation. (The $\cos b$ or $\cos\delta$ factor implied by the asterisk is never differentiated; thus $\partial{l*}/\partial\alpha*=(\partial l/\partial\alpha)\cos b/{\cos\delta}$ , etc.) Clearly $\text{E}\left[\boldsymbol{g}\right]=\boldsymbol{J}\text{E}\left[\boldsymbol{e}% \right]=\boldsymbol{0}$ , so the galactic parameters are also unbiased, with covariance matrix

\boldsymbol{C}_{\text{Gal}}=\text{E}\left[\boldsymbol{g}\boldsymbol{g}^{\prime% }\right]=\boldsymbol{J}\boldsymbol{C}\boldsymbol{J}^{\prime}\,.

(3.28)

It remains to determine $\boldsymbol{J}$ . Since $\varpi$ is unchanged by the transformation we have $J_{22}=1$ and $J_{i2}=J_{2i}=0$ for $i\neq 2$ . It is also readily seen that the proper motion errors transform in the same way as the positional errors (if we regard $\boldsymbol{p}$ and $\boldsymbol{q}$ as fixed and not subject to errors); then from Equation 3.16–Equation 3.20 we find

\boldsymbol{J}=\begin{bmatrix}\boldsymbol{G}&0&0\\ 0&1&0\\ 0&0&\boldsymbol{G}\end{bmatrix}

(3.29)

where

\boldsymbol{G}=\left[\boldsymbol{p}_{\text{Gal}}\quad\boldsymbol{q}_{\text{Gal% }}\right]^{\prime}\boldsymbol{A}_{\text{G}}^{\prime}\left[\boldsymbol{p}_{% \text{ICRS}}\quad\boldsymbol{q}_{\text{ICRS}}\right]

(3.30)

is an orthogonal $2\times 2$ matrix. Geometrically, $\boldsymbol{G}$ describes the local rotation from ICRS to galactic coordinates in the tangent plane of the celestial sphere at the position of the source.

3.1.8 Fundamental constants

Author(s): Jos de Bruijne

The Gaia data processing makes use of a large number of constants and parameters. These vary from mathematical constants, through constants of nature, to parameters describing the instrument (for instance the number of CCD rows). To keep track of constants and parameters in a controlled way, all data processing software interfaces to the Gaia Parameter Data Base (Section 1.2.5; Perryman et al. 2008). This data base is updated regularly (under configuration control) and is based on industrial design documents and other sources of information. DR1 in particular uses IAU resolutions up to and including 2012, the 2010 version of the CODATA recommended values of the fundamental physical constants (Mohr et al. 2012), and the INPOP10e solar-system ephemerides (Section 3.2.1; Fienga et al. 2016, 2011).

European Space Agency

Science & Technology

3.1 Introduction

3.1.1 Overview

3.1.2 Conventions, notations, nomenclature, and definitions

Physical units: The SI system

Notation of units

Acronyms

3.1.3 Reference systems and time scales

3.1.4 Standard model of stellar motion

3.1.5 Relativistic model

3.1.6 Time scales

3.1.7 Transformations of astrometric data and error propagation

Galactic coordinates

Transformation of position

Transformation of proper motion

Error propagation

3.1.8 Fundamental constants

Copyright 2024 © European Space Agency. All rights reserved.