4.4.6 AGIS-PhotPipe-IDU loop processing
Author(s): Uwe Lammers, Alex Bombrun
The quality of an astrometric solution computed by AGIS is directly related to the quality of the input data, see Section 4.2. The most fundamental quantities in this regard are the astrometric along scan observations, which translate to transit times per CCD. A transit time is the time when the centroid of the LSF/PSF of an observed source crosses in the along scan (AL) direction a fiducial line, a nominal position for each gate on every CCD, see Section 4.3.6 for a detail description of the astrometric observations.
A first determination of the transit times is done in the Initial Data Treatment (IDT), see (Fabricius et al. 2016) that runs as part of the daily processing of all incoming telemetry from Gaia at DPCE, see Section 3.4.2. Although AGIS can use IDT data in principle, in really relies on IDU for improved and consistent centroids. A description of the top-level functionalities of IDU can be found in Section 3.4.2. The IDU centroid computation is done through a process called IPD (Image Parameter Determination) which fits parameterized LSF templates to the observed CCD sample data. One of the fitted quantities is the sought position of the centroid within the window (composed of raw CCD sample data) of the observation which then gets converted into a time. The LSF/PSF templates used in IDU are described in Section 3.3.5.
Besides centroids, the other IDU output, critical for any astrometric solution, is the global crossmatch (XM) which assigns observations to sources, see Section 3.4.13. The effect of a wrong-XM on AGIS is that the set of observations belonging to the same physical source might be split among two or more real or spurious sources. As a result, the number of observations of the real source is lower and the number of outliers higher than it ought to be resulting in the astrometric solution for that source being consequently weaker. If a source ends up with too few observations due to a wrong XM result, the astrometry for that source might be of very poor quality (large formal errors). As a result some sources may have a 2 parameters fallback solution or even no astrometric solution.
The PSF/LSF calibration, IPD determination and global crossmatch in IDU benefit from AGIS’s improved geometric calibration and improved astrometry, and also from improved source colours and magnitudes from PhotPipe, see Chapter 5. IDU, like AGIS and PhotPipe, is part of the so-called DPAC cyclic processing. This is schematically illustrated in Figure 4.18.
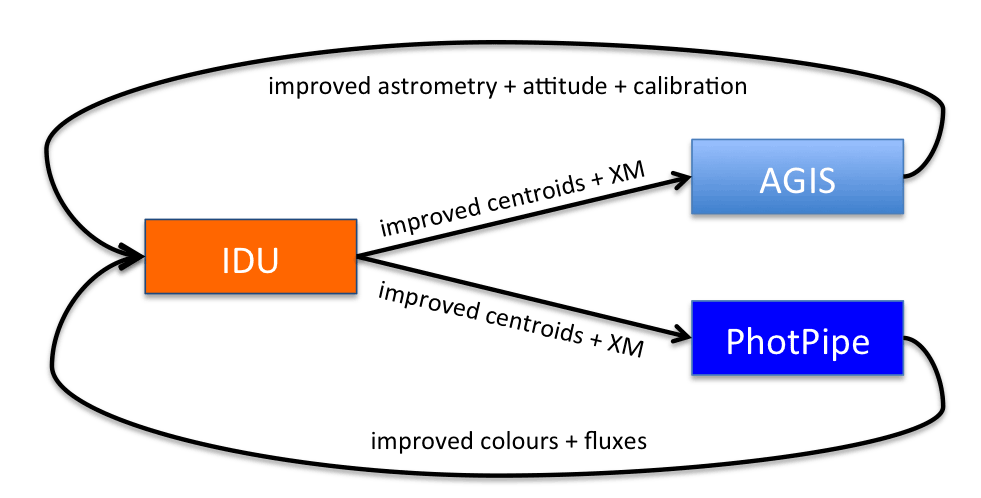
It represents the decisive overall iterative loop of the Gaia core processing expected to converge towards better and better astrometric solutions with time and the inclusion of increasingly more observation data as the mission progresses.
For Gaia EDR3, IDU’s LSF/PSF libraries were more mature than in earlier cycles and the AGIS-PhotPipe-IDU loop processing has begun to be iterated. Although the calibration model of AGIS still included chromatic terms, they were now much smaller especially for WC1 and WC2 observations (see Section 4.5.5). This shows that the AGIS-PhotPipe-IDU loop converges quite rapidly although the calibration models for WC0 observations need to be much improved, probably both on the IDU and AGIS sides, before convergence is possible in the bright regime. With the forthcoming data reduction cycles, IDU’s LSF/PSF libraries should become more and more complex and precise relying on improved magnitude and colour. Ultimately, the goal is to remove the need for any chromatic and magnitude effect in the AGIS calibration.
Once the operational phase of the mission is concluded and no more input data arrive the looping will still have to continue for a while before the results settle. This is a consequence of the cyclic nature of the processing in DPAC. Not only will each system use an older version of the other systems output, but the whole loop should be iterated in order to converge. The AGIS-PhotPipe-IDU loop processing is the keystone of the DPAC core processing and a fundamental step to build the final Gaia astrometric solution.