9.4.1 Light profile models

Two models are successively fitted on the galaxies: a free Sérsic profile, and a de Vaucouleurs profile (Sérsic profile with index $n=4$). An exponential profile (equivalent to a Sérsic profile with index $n=1$) has also been adjusted but is not published in the Gaia DR3 (see Section 9.7.1):

• •

  Sérsic:

  $$\mathrm{I}(\mathrm{r})={\mathrm{I}}_{Re}\exp \left(-b_n\left({(\mathrm{r}/Re)}^{1/n}-1\right)\right),$$

  
  

  where ${\mathrm{I}}_{Re}$ is the light intensity at the effective radius $Re$, $Re$ is the major-axis effective radius encompassing half of the total flux of the source, n is the Sérsic index, $b_n$ is a constant depending on n and r is the radius where the intensity is computed. $b_n$ is calculated by using the analytical approximation from Capaccioli (1989) and Graham et al. (2005), $b_n=1.9992n-0.3271$, which is valid for a large range of Sérsic indexes (0.5 10).

• •

  de Vaucouleurs:

  $$\mathrm{I}(\mathrm{r})={\mathrm{I}}_{Re}\exp \left(-7.6697\left({(\mathrm{r}/Re)}^{1/4}-1\right)\right),$$

where $n$ corresponds to n_sersic, ${\mathrm{I}}_{Re}$ to intensity_sersic for the Sérsic profile, intensity_de_vaucouleurs for the de Vaucouleurs profile, $Re$ to radius_sersic for the Sérsic profile, intensity_de_vaucouleurs for the de Vaucouleurs profile

The central quasar is described by a circular exponential profile with a fix scale length ${\mathrm{r}}_d=39.4$ mas (which approximately corresponds to the line spread function of Gaia and thus well represents a point-like source) and the host galaxy is represented by a free Sérsic profile.

• •

  Central quasar: ${\mathrm{I}}_q(\mathrm{r})={\mathrm{I}}_C\exp (-\mathrm{r}/{\mathrm{r}}_d$)
  

• •

  Host galaxy: ${\mathrm{I}}_g(\mathrm{r})={\mathrm{I}}_{Re}\exp \left(-b_n\left({\left(\frac{\mathrm{r}}{Re}\right)}^{1/n}-1\right)\right)$

where $n$ corresponds to the sersic_index, $Re$ to radius_hostgalaxy, ${\mathrm{I}}_{Re}$ to intensity_hostgalaxy,
${\mathrm{I}}_C$ to intensity_quasar (at centre).

For both galaxies and host galaxies of quasars an ellipticity ‘e’ and a position angle ‘PA’ (shape parameters hereafter) are also searched for. This is implemented following, for example, Athanassoula et al. (1990) by computing the intensities at the radius:

with $x_p=x\cos (PA)-y\sin (PA)$ and $y_p=x\sin (PA)+y\cos (PA)$ and $e=1-b/a$ with a and b being the major and minor axis of the elliptic profile.

Concerning the galaxies, the fitted shape parameters are provided in ellipticity_sersic for the ellipticity of the Sérsic profile, ellipticity_de_vaucouleurs for the ellipticity of the de Vaucouleurs profile, and posangle_sersic for the position angle of the Sérsic profile, posangle_de_vaucouleurs for the position angle of the de Vaucouleurs profile.

Concerning the host galaxy of the quasars, the fitted shape parameters are provided in ellipticity_hostgalaxy for the ellipticity and posangle_hostgalaxy for the position angle.

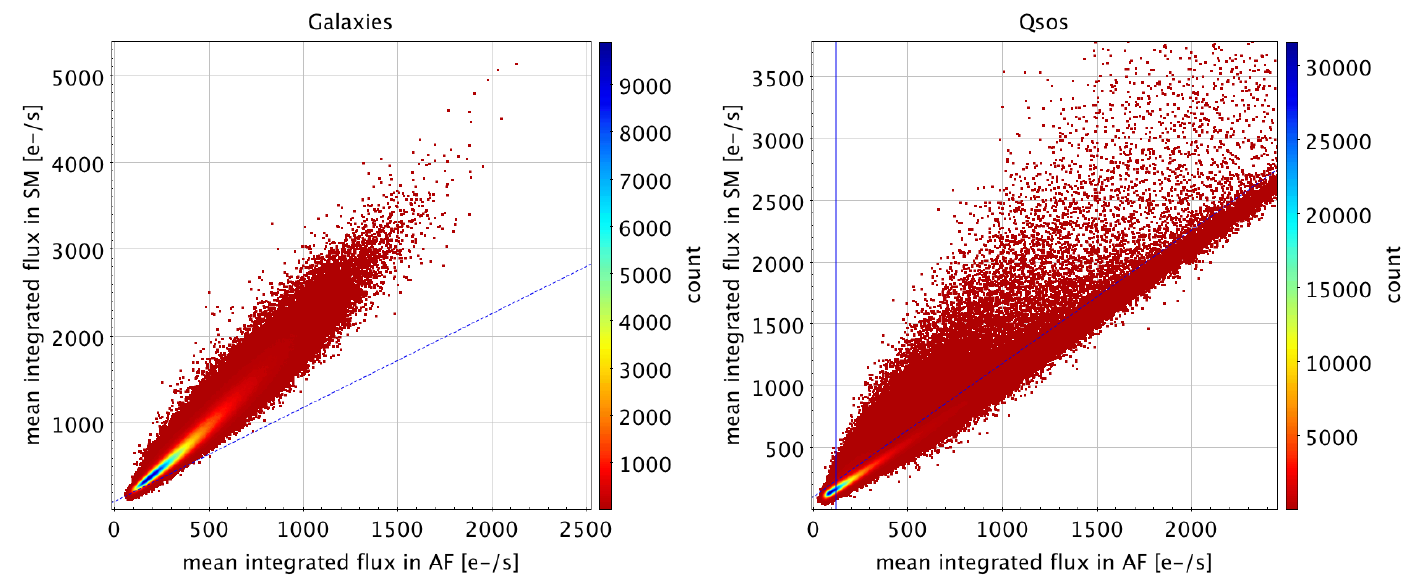
For both host galaxies of quasars and galaxies, a sub-sample of the input lists have been identified as too faint for any tentative measurement of ellipticity and position angle. These sources are then fitted with circular profiles and thus the fields corresponding to ellipticity and position angle are not provided. The comparison of the mean integrated flux over all transits in the AF median window and the SM window allows to determine the limit where it is no more possible to retrieve an ellipticity as shown in Figure 9.4. Most galaxies considered here have a mean integrated flux in the SM window superior to that in the median-AF window indicating that these objects extend beyond the limit of the AF window. It has been empirically determined that the line of equation : flux(SM) flux(AF) + 100 (blue line in Figure 9.4) isolates objects unsuited for a determination of ellipticity. Most quasars have a similar flux in both detectors and are likely to be tiny or point-like with undetectable ellipticity with Gaia. For this class of objects with flux(SM)1.06$\times$flux(AF)+200 a circular profile is fitted for the host galaxy. This limit has been empirically set. Objects with larger fluxes in the SM detector usually exhibit an extension and a potentially measurable ellipticity. For these (flux(SM)$>$1.06$\times$flux(AF)+200 ) an elliptical profile is fitted for the host galaxy. Quasars with low fluxes in the median-AF (flux(AF) ) appear immeasurable due to their low level of signal to noise. These sources are then not processed and considered afterward as point-like with no host galaxy detectable by our algorithm.