2.4.5 On-ground attitude reconstruction (IOGA, OGA1, and OGA2)
Author(s): David Hobbs, Michael Biermann, Jordi Portell
The processing of attitude telemetry from the Gaia spacecraft is unique due to the high accuracy requirements of the mission. Normally, for science missions, the on-board measured attitude from the star trackers, in the form of attitude quaternions, would be sufficient for the scientific data reduction but perhaps requiring some degree of smoothing and improvement before use. Such a raw attitude would be accurate to the order of a few arcseconds ( ) but for the Gaia mission, an attitude accurate to a few tens of as is required. This is achieved through a series of processing steps as illustrated in Figure 2.10.
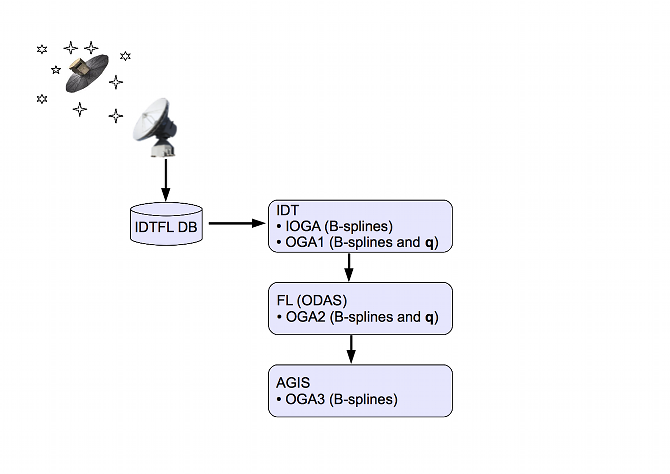
The raw attitude is received in telemetry and stored in the IDTFL database. This is then available for IDT, which first performs the Initial On-Ground Attitude (IOGA) reconstruction, which fits a set of B-spline coefficients to the available telemetry, resulting is an array of B-spline coefficients and the associated knot times (see Section 3.3.5). The output from IOGA can then be used as the input to the First On-Ground Attitude (OGA1) reconstruction, which is a Kalman filter designed to smooth the attitude and to improve its accuracy to the order of 50 mas. At this point, more Gaia specific processing begins. For Gaia, a First Look (FL) process is employed to do a direct astrometric solution on a single days worth of data, known as the One Day Astrometric Solution (ODAS). This is basically a quality check on the Gaia data but also results in an order of magnitude improvement in the accuracy of the attitude. After ODAS, the attitude is known as OGA2 and is available in the form of B-splines and quaternions. OGA2 is the intended nominal input to AGIS, although it would also be possible to use OGA1 from IDT as input to AGIS. However, in practice, mainly due to data gaps and discontinuities between OGA1 segments, it has been found that a simple spline fit to the commanded attitude is sufficient for initializing AGIS processing. AGIS is the the final step in the attitude improvement, where all the available observations for primary stars are used together with the available attitude and calibration parameters to iteratively arrive at the final attitude solution. This AGIS final attitude is referred to as the OGA3 (Section 3.3.5).
The attitude related tasks in IDT are (see Section 2.4.2):
-
•
ingest the auxiliary science data (ASD), star packets (SP1) for the brightest detections ( mag), and raw attitude from the IDTFL database, noting the time intervals covered;
-
•
compute the Initial OGA (IOGA) for suitable time intervals;
-
•
extract a list of sources from the Attitude Star Catalogue (Section 2.2.3) using IOGA, and identify (crossmatch) those sources corresponding to the mentioned bright detections;
-
•
determine OGA1 by correcting IOGA with the match distances to the catalogue by means of an Extended Kalman Filter (EKF).
IOGA
In IDT, the raw attitude values from the AOCS are processed to obtain a mathematical representation of the attitude as a set of spline coefficients. The details of the spline fitting are outlined in Appendix A of Lindegren et al. (2012). The result of this fitting process is the Initial OGA (IOGA). The time intervals processed can be defined by natural boundaries, like interruptions in the observations, e.g., due to micro-meteorites. The boundaries can also be defined by practical circumstances, like the end of a data transmission contact, or the need to start processing.
Using IOGA, a list of sources is extracted from the Attitude Star Catalogue (ASC; Section 2.2.3) in the bands covered by Gaia during the time interval being processed. In the early phases of the mission (for Gaia DR1), the ASC was a subset of the IGSL, but in Gaia DR2, the ASC has been replaced by stars from the MDB catalogue. This allows the next process, OGA1, to run efficiently, knowing in advance if a given observation is likely to belong to an ASC star.
OGA1
The main objective of OGA1 is to reconstruct the non-real-time First On-Ground Attitude (OGA1) for the Gaia mission with high accuracy for further processing. The accuracy requirements for the OGA1 determination (along and across scan) are 50 mas (to be improved later on in the mission to 5 mas). OGA1 relies on an Extended Kalman filter (EKF) to estimate the orientation, , and angular velocity, , of the spacecraft with respect to the Satellite Reference System (SRS), defining the state vector
| (2.6) |
System model
The system model is fully described by two sets of differential equations, the first one describing the satellite’s attitude following the quaternion representation
| (2.7) |
where
| (2.8) |
and the second one using the Euler’s equations:
| (2.9) |
where is the moment of inertia of the satellite and is the total of disturbance and control torques acting on the spacecraft. The satellite is assumed to be represented as a freely rotating rigid body, which implies to set the external torques to zero in Equation 2.9. If this simplification does not work well when reconstructing the Gaia attitude then the proper , including external torques, that is required to follow the NSL should be taken into account.
Process and measurement model
The process model predicts the evolution of the state vector and describes the influence of a random variable , the process noise. For non-linear systems, the process dynamics is described as follows:
| (2.10) |
where and are functions defining the system properties. For OGA1, is given by Equation 2.7 and Equation 2.9, and is a discrete Gaussian white noise process with variance matrix :
| (2.11) |
The measurement model relates the measurement value to the value of the state vector and describes also the influence of a random variable , the measurement noise of the measured value. The generalized form of the model equation is:
| (2.12) |
where is the function defining the measurement principle, and is a discrete Gaussian white noise process with variance matrix (with standard deviations of 0.1 mas and 0.5 mas along and across scan respectively):
| (2.13) |
In order to estimate the state, the equations expressing the two models must be linearized in order to use the KF model equations, around the current estimation () for propagation periods and update events.
This procedure yields the following two matrices to be the Jacobian of the and functions with respect to the state:
| (2.14) |
and
| (2.15) |
KF propagation equations
The KF propagation equations consist of two parts: the state system model and the state covariance equations. The first one,
| (2.16) |
can be propagated using a numerical integrator, such as the fourth-order Runge-Kutta method. The matrix is called the transition matrix, the system noise covariance matrix, and the system noise covariance coupling matrix.
The transition matrix can be expressed as:
| (2.17) |
where
| (2.18) |
and
| (2.19) |
Here, the matrix notation represents the skew symmetric matrix of the generic vector . For the state covariance propagation, the Riccati formulation is used:
| (2.20) |
Its prediction can be carried out through the application of the fundamental matrix (i.e., first order approximation using the Taylor series) about , which becomes:
| (2.21) |
where represents the propagation step. The process noise matrix used for the Riccati propagation Equation 2.20 is considered to be
| (2.22) |
since OGA1 depends more on the measurements (even if not so accurate at this stage) than on the system dynamic model.
KF update equations
The KF update equations correct the state and the covariance estimates with the measurements coming from the satellite. In fact, the measurement vector consists of the so-called measured along-scan angle , and the measured across-scan angle , and they are the values as read from the AF1 CCDs.
On the other hand, the calculated field angles () are the field angles calculated from an ASC for each time of observation. The set of the update equations are listed below:
| (2.23) | |||
| (2.24) | |||
| (2.25) |
where the measurement sensitivity matrix is given by:
| (2.26) |
and the measurement noise matrix is chosen such that:
| (2.27) |
The standard deviation for the field angle errors along and across scan are computed and provided by IDT.
The processing scheme
The OGA1 process can be divided in three main parts: input, processing, and output.
The inputs are:
-
•
Oga1Observations (OGA1 needs these in time sequence from IDT) composed essentially by:
-
–
transit identifiers (TransitId)
-
–
observation times (TObs)
-
–
observed field angles (FAs) including geometry calibration
-
–
-
•
A raw attitude (IOGA), with about 7 noise (in B-splines).
-
•
A crossmatch table with SourceId–TransitId pairs plus a proper direction to the star at the instance of observation.
The OGA1 determination is a Kalman Filter (KF) process, i.e., essentially an optimization loop over the individual observations, concluded by a spline-fitting of the resulting quaternions. The main processing steps are:
-
•
Sort the list of elementaries by time. Then sort the list of crossmatch sources by the transit identifier with the ones from the sorted list of elementary. The unmatched elementary transits are simply discarded.
-
•
Initialize the KF: interpolate the B-spline (IOGA attitude format) in order to get the first quaternion and angular velocity to start the filter. Optionally, the external torque can be reconstructed in order to have a better accuracy for the dynamical system model.
-
•
Forward KF: for a generic time , predicting the attitude quaternion from the state vector at the time of the preceding observation.
-
•
Backward KF: for a generic time , predicting the attitude quaternion from the state vector at the time of the preceding observation. Backward propagation is needed to reduce errors near the start of the time interval.
-
•
Compute the field coordinates from the pixel coordinates for SM and AF measurements, using a Gaia calibration file. OGA1 uses the AF2 values as observed field angles.
-
•
Compute field coordinates of known stars (from the ASC).
-
•
Correct the state using the difference between the observed and the calculated measurements in the along-scan () and across-scan () directions.
-
•
Generate a B-spline representation for the whole time interval at the end of the loop over the measurements.
-
•
Remove any attitude spike that may appear, for example due to a wrong crossmatch record.
The outputs are the improved attitude (for each observation time ) in two formats:
-
•
Quaternions in the form of arrays of doubles.
-
•
A B-spline representation from the OGA1 quaternions.
The OGA1 process, being a Kalman filter, needs its measurements in strict time sequence. In order to keep the OGA1 process simple, the baseline is to separately use the CCD transits. OGA1 relies on two-dimensional (2D) astrometric measurements from Gaia. That is, CCD transits of stars used by OGA1 must have produced 2D windows. OGA1 furthermore requires at least about one such 2D measurement per second and per FoV, in order to obtain the required precision.
OGA2 and ODAS source positions
The main objective of the ODAS is to produce a daily, high-precision astrometric solution that is analysed by First Look Scientists in order to judge Gaia’s instrument health and scientific data quality (see also Section 2.5.2). The resulting attitude reconstruction, OGA2, together with source position updates computed in the framework of the First Look system, is also used as input parameter by the photometric and spectroscopic wavelength calibrations (for the last mission data segment in each Gaia data release). For the first two data segments (Table 1.4), OGA2 is accurate to the 50 mas level because it is (like OGA1) tied to the reference system of the ground-based ASC, but it is precise at the sub-mas level, i.e., internally consistent, except for a global rotation with respect to the ICRF. The OGA2 accuracy will improve during the mission with each catalogue produced by DPAC.
The computation of OGA2 is not a separate task but one of the outputs of the ODAS (One-Day Astrometric Solution) software of the First Look System (see Section 2.5.2). This process can be divided into three main parts: input, processing, and output:
-
1.
The OGA2 inputs are outputs of the IDT system, namely:
-
–
AstroElementaries with transit IDs and observation times,
-
–
OGA1 quaternions ,
-
–
a source catalogue with source IDs, and
-
–
a crossmatch table with pairs of source IDs and transit IDs.
-
–
-
2.
The processing steps: the OGA2 attitude is determined in one go together with daily geometric instrument calibration parameter updates and updated source positions in the framework of the First Look ODAS system (which is a weighted least-square method).
-
3.
The OGA2 output is a B-spline representation of the improved attitude (as a function of observation time ).
Along with OGA2, First Look produces on a daily basis improved sources positions which also are used as input parameters by the photometric and spectroscopic wavelength calibrations (for the last mission data segment in each Gaia data release). The accuracy and precision levels of the source positions are the same as those of OGA2.