8.3.1 Effective temperatures
Author(s): René Andrae
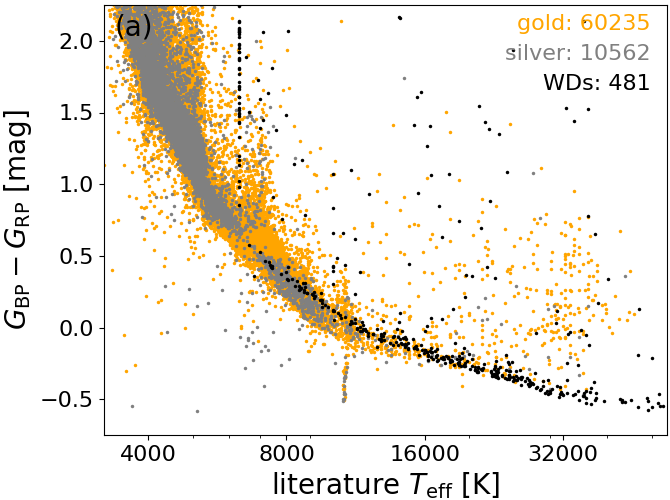
We estimate stellar effective temperatures, , from the two distance-independent colours and . These two colours are rather degenerate, as is obvious from the tight locus in Figure 8.1. Nonetheless, the synthetic photometry shown in Figure 8.1a reveals a clear dependence of colours on temperature with , which is confirmed by the colours of real Gaia stars with literature estimates of shown in Figure 8.2.
 |
 |
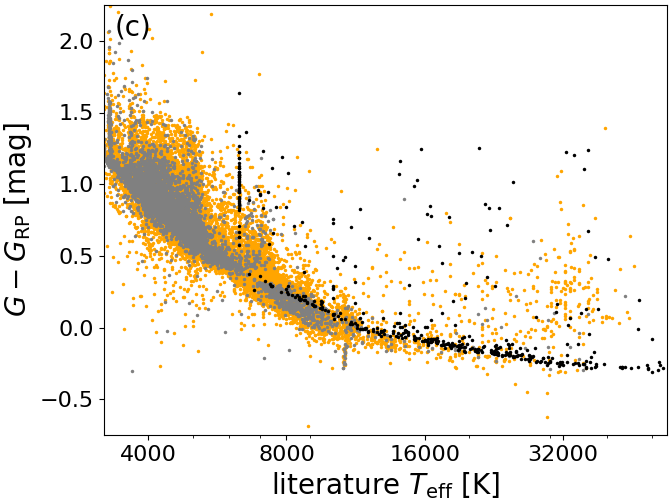 |
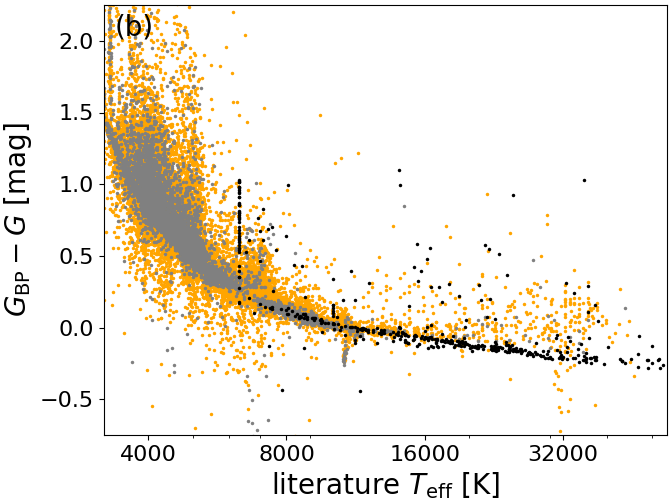
It is possible to form a third colour, , but this is not independent of the other two colours. More importantly, is noisier than the other two colours since it does not contain the -band which has higher signal-to-noise ratio because the astrometric field has more CCDs (Gaia Collaboration et al. 2016).
All three possible colours exhibit monotonic colour-temperature relations, as shown in Figure 8.3. As an aside, let us emphasise that Figure 8.3 also demonstrates that gold-standard and silver-standard photometry indeed provide the same colour-temperature relations. This is an independent validation of the gold and silver photometric system (Riello et al. 2018).
For our temperature estimation, we refrain from using a simplistic polynomial model, which would make too restrictive a-priori assumptions about the mathematical form of the colour-temperature relation. Instead, we use and as features to estimate using extremely randomised trees (Geurts et al. 2006, hereafter ExtraTrees). This machine-learning algorithm comes up with a non-parametric model for the colour-temperature relation, which is far more general than a model of polynomial class. We do ExtraTrees regression with an ensemble of 201 trees, whose median value provides the parameter estimate. Further ExtraTrees regression parameters are random trials per split and minimal stars per leaf node. Furthermore, as uncertainty estimates, we provide the 16th and 84th percentiles of the ExtraTrees ensemble, which form a central 68% confidence interval. These uncertainty estimates in general form an asymmetric confidence interval. Note that we do not propagate the flux errors through ExtraTrees such that the reported uncertainty interval is solely due to the degeneracy of with the colours as well as the intrinsic spread of the ExtraTrees ensemble. However, off-line testing has shown that propagating the flux errors through ExtraTrees has only little impact on the resulting parameter or uncertainty estimates. Let us also emphasise that ExtraTrees are incapable of extrapolation, i.e. if its training sample has a limited range of labels, ExtraTrees can never produce parameter or uncertainty estimates outside this training label range.
| percentile | 5th | 50th | 95th |
| [mag] | 0.056 | 0.335 | 0.705 |
| [mag] | 0.04 | 0.13 | 0.32 |
Since the real in-flight instrument differs from the nominal pre-launch prescription (Jordi et al. 2010), we cannot train ExtraTrees on synthetic photometry. Instead, we train on 32 602 real stars with observed Gaia photometry and labels provided by the literature. The empirical training sample is restricted to the range 3000K10 000K, since outside this interval there are not enough stars with literature estimates of to train good ExtraTrees models. Since ExtraTrees cannot extrapolate, this implies that there are no sources in Gaia DR2 with with K or K. Since this training sample is empirical, the real stars have non-zero extinctions which are estimated from the literature (where available) in Table 8.2. Evidently, the properties of this empirical training sample – its limited range, the details of its distribution, but also the non-zero extinction – will all have an impact on the resulting temperature estimates. For further details see Andrae et al. (2018).