8.3.3 Stellar luminosities and radii
Author(s): Orlagh Creevey, Christophe Ordenovic
Stellar radii and luminosities are estimated as part of the FLAME software package. The luminosities are derived using
| (8.6) |
where is given in solar units, is given by Equation 8.1, as defined by the IAU Resolution 2015 B2 and is the temperature-only dependent bolometric correction. is then calculated from and (see Equation 8.2).
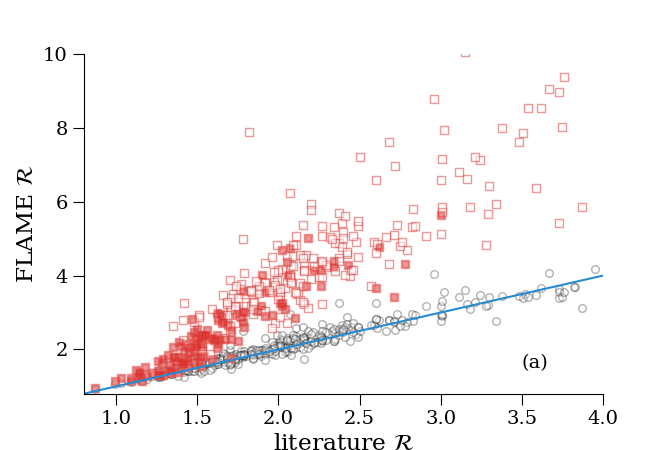
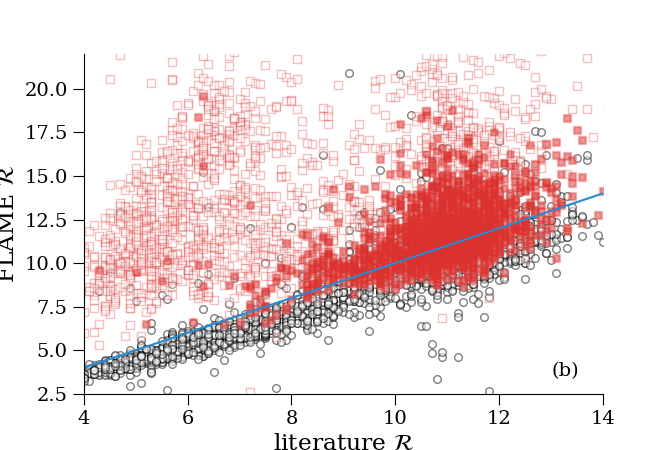
The Priam estimates are found not be very accurate on a star-to-star basis. This is shown in Figure 8.7 where we compare with those values taken from external catalogues for main sequence (panel a, Chaplin et al. 2014) and more evolved stars (panel b, Vrard et al. 2016). Black represents as found in Gaia DR2, i.e. setting = 0.0 mag, and red represents using from Priam (Equation 8.8). It can be seen that including Priam leads to an overestimation of (and ) for many stars. For this reason we decided to set = 0.0 mag in Equation 8.1 to derive the radius and luminosity for Gaia DR2. On the right panel it can be seen, however, that in some cases, e.g. stars with 11 , better agreement with the literature is obtained when we use from Priam (the bisector passes closer to the mean of the points). Upon validation of the astrophysical parameters, it was decided to remove and from Gaia DR2 for some sources satisfying certain conditions (Andrae et al. 2018). This removed many of the outliers in these figures. The sources with the filled red squares are the sources with an estimate in Gaia DR2.
Should a user want to estimate luminosity or radius assuming a non-zero extinction and/or a change in the bolometric correction of , one can use the following expressions
| (8.7) |
| (8.8) |
We obtained our bolometric correction on a grid as a function of , , [Fe/H], and [/Fe], derived from the MARCS synthetic stellar spectra (Gustafsson et al. 2008) for a range 2 500K to 8 000K. The spectra were calculated for values of between and +5.5 dex, [Fe/H] between and dex, and [/Fe] between +0.0 and +0.4. The magnitudes are then computed from the grid spectra using the filter (see Figure 5.9). These models assume local thermodynamic equilibrium (LTE), with plane-parallel geometry for dwarfs and spherical symmetry for giants. We extended the range using the from Jordi et al. (2010), but with an offset added to achieve continuity with the MARCS models. However, following validation of our results we choose to filter out FLAME results for stars with outside the range 3300 – 8000 K.
For the present work we have two issues to address. First, is a function of four parameters which we do not have at our disposition in Gaia DR2, and so we must derive a 1D temperature projection. The second issue concerns the bolometric correction offset, as this is not defined by the synthetic models.
-
1.
To address the first issue we selected the models with [/Fe] = 0 and . For each bin we adopted the mean value of the selected as and the dispersion primarily due to as the standard deviation . We then fit a polynomial to these values to define a function ()
(8.9) This was done in two temperature regions 2500 – 4000 K and 4000 K – 8000 K. The bolometric correction is shown in Figure 8.8, and the resulting coefficients are given in Table 8.3, where we have fixed the the offset parameter as the reference bolometric correction of the Sun () = +0.06.
Table 8.3: Polynomial coefficients of the model defined in Equation 8.9 (column labelled ). A separate model was fit to the two temperature ranges, with for the hotter temperature range fixed to the value given. The column labelled lists the coefficients for a model of the uncertainty in the fit. (Andrae et al. 2018). for for 4000–8000 K 6.000 2.634 6.731 2.438 6.647 1.129 2.859 6.722 7.197 1.635 3300–4000 K 1.749 2.487 1.977 1.876 3.737 2.128 8.966 3.807 4.183 6.570 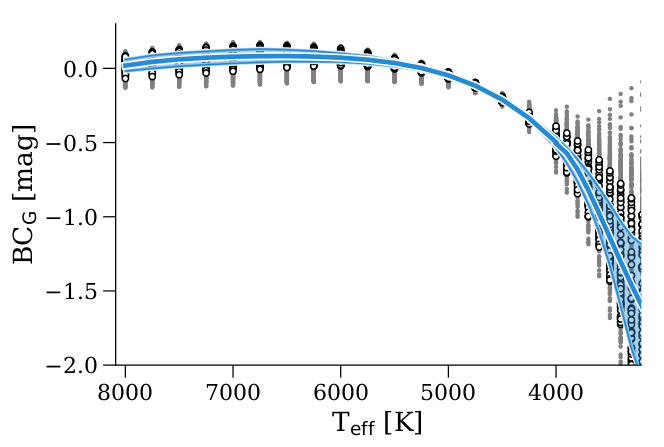
Figure 8.8: Bolometric corrections from the MARCS models (grey dots) and the subset we selected (open circles) to fit the polynomial model (Equation 8.9, with fixed ), to produce the blue line and the associated 1- uncertainty indicated by the blue shaded region. (Andrae et al. 2018). -
2.
The conversion of to depends on the photometric filter and the subsequent data treatment. As we have no single reference star for which we know and (through the observed ) exactly, we need to determine it empirically in order to set the scale. In the ideal case we use the solar value through a conversion to derive (), and correct () in order to obtain the solar value at 5772 K. However, at the time of processing no conversion was available, and we opted for an empirical determination.
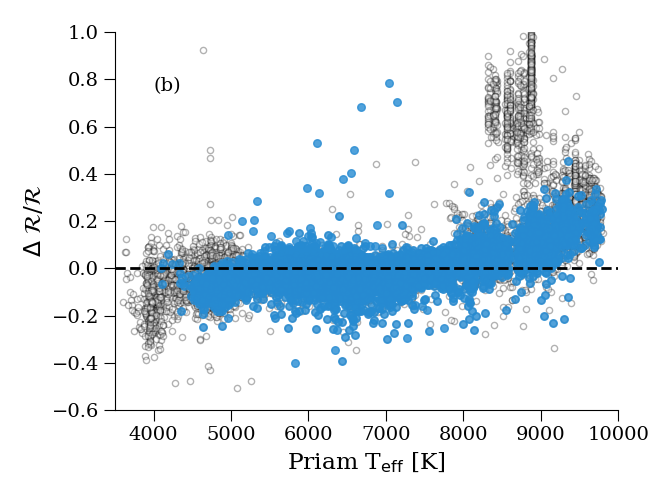
Our empirical determination consisted of selecting several catalogues with stars where we can assume is near zero or we can assume a single value for the population. Of these stars we further selected the cleanest subsamples by choosing sources with , , and . We then corrected for the differences in Priam and the values from the external catalogue in order to isolate the effect of on the radius. The () was fitted for each subsample by minimizing the differences between FLAME and literature radii and luminosities values. After performing this analysis on several subsamples along with subsequent validation we obtained a mean () = +0.060.10 mag. This implies that here in this work mag and consequently = –0.13 mag using Torres (2010). Figure 8.9 shows a comparison between the literature and FLAME luminosity and radius after setting () = +0.06 mag. The open symbols in panels (a) and (b) show luminosities using published bolometric fluxes from Casagrande et al. (2011), and radii using predicted angular diameters from Bourges et al. (2017), respectively. The filled symbols show the subset of sources which were used to determine (). By construction, the mean differences are close to zero, and we find a disperion below % in both and , indicating no unknown systematic effects in our results. More detail is given in the appendix of Andrae et al. (2018). For above 8 000 K (panel b) the differences may be attributed to a poorer calibration of this temperature range for predicting angular diameters. Equally the discrepancy can be attributed to these stars having Gaia photometry outside of the training range. Note that we do not publish or for sources with above 8000 K.

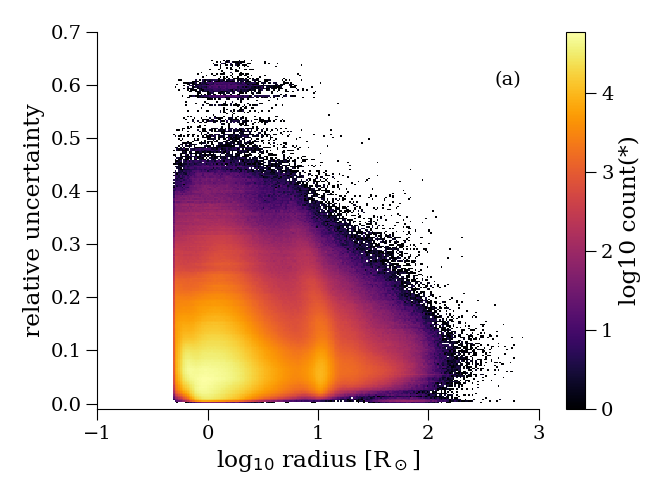
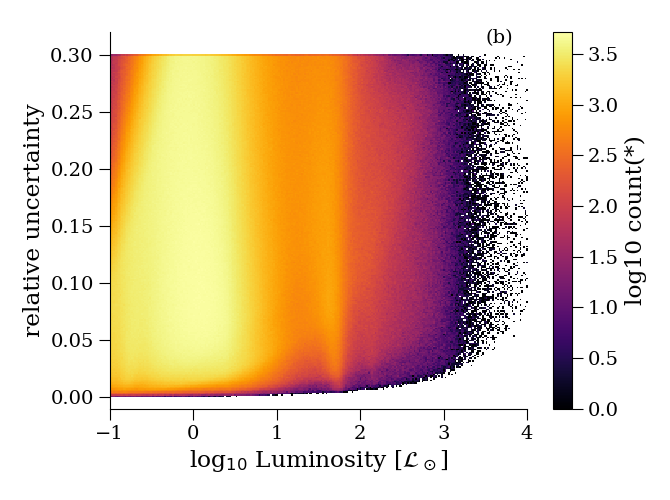
The 1- uncertainties in are based on a first order propagation of uncertainties considering and . These are reported in the catalogue as a symmetric confidence interval. The lower and upper radius percentiles is obtained from propagating through the values of the lower and upper percentiles. The distribution of the relative uncertainties as a function of and is shown in Figure 8.10.