skip to main content

gaia data release 3 documentation

7.6 Eclipsing binaries

7.6.6 Known issues

This is the first data release that includes EB orbital solutions and, as already mentioned earlier, there has only been a limited time to validate them or even properly address the problems that were discovered. One way to mitigate this situation was to limit the published sample to a small fraction of the original that satisfies a set of filtering criteria (cf. Section 7.6.5). However, even with this higher quality sample, there are a number of lingering issues and concerns of which the end user should be aware, and are discussed in this section.

Apparent inconsistency between 𝐅𝟐 and the overall quality of the fit

Perhaps the most obvious issue concerns the goodness-of-fit statistic, F⁢2, which remains consistently high for most solutions (see Figure 7.53), thus giving the impression that most of them do not fit the data well. The reason for this is not entirely clear. F⁢2 should follow the normal distribution 𝒩⁢(0,1) if the physical model applied is adequate, if the least-squares algorithm is capable of converging to the best fit, and if the estimates of the measurement uncertainties are right. There certainly are solutions where the fit is genuinely bad, most likely due to global optimisation failing to find a suitable reference LC. However, most such solutions have been filtered out by the process described in Section 7.6.5.

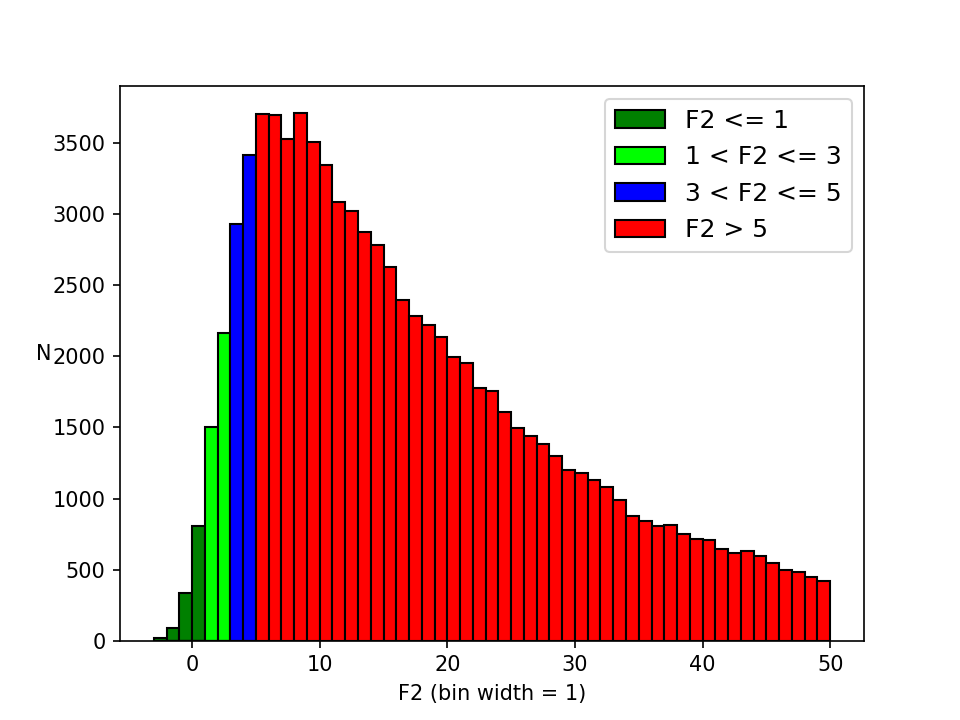
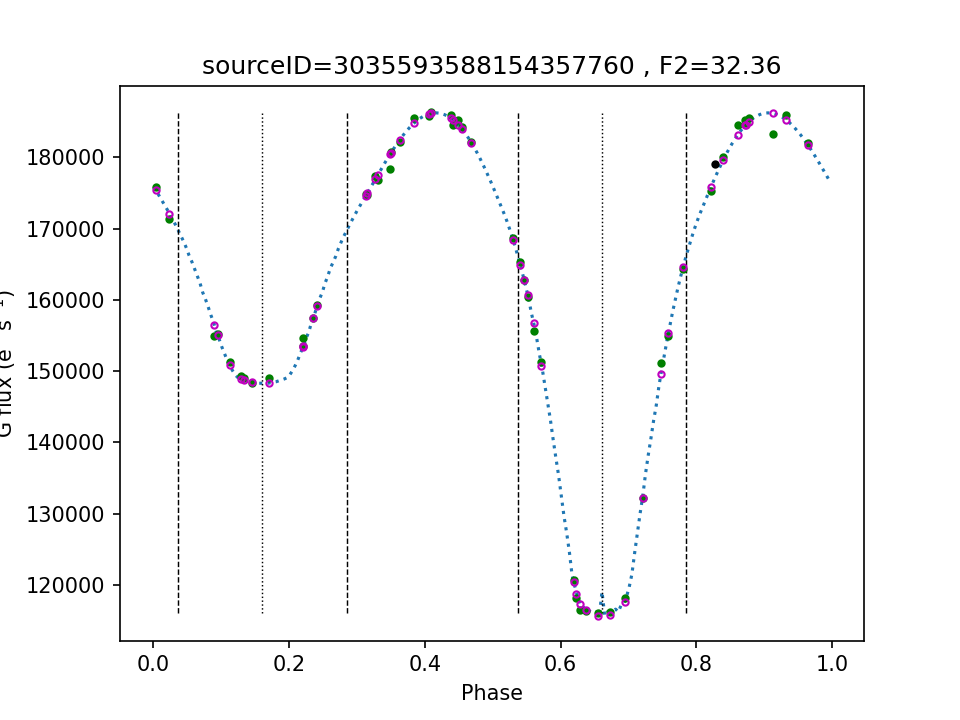
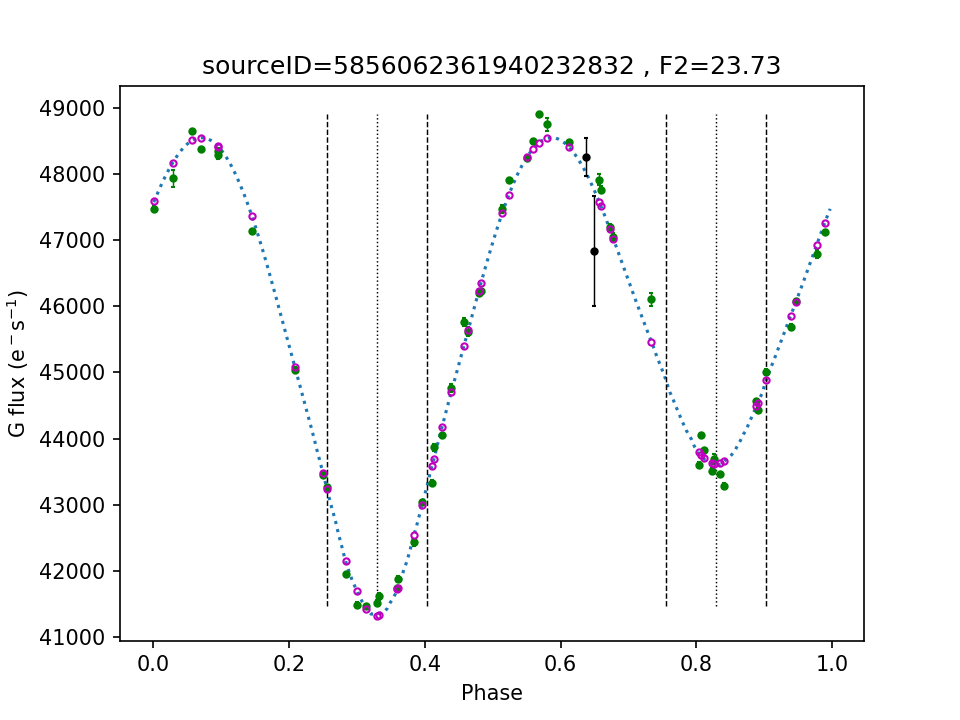
Figure 7.53: The distribution of the goodness-of-fit statistic F⁢2. Solutions with F⁢2>50 are filtered out of Gaia DR3. The distribution exhibits a peak around F⁢2≈5-9 followed by a long tail of higher values. Although it is likely that these high values are partly attributable to genuine shortcomings in the fitting procedure or in the physical model behind it, it is also possible that they are affected by unrealistically small uncertainties in the photometry of the light curves.

Figure 7.54 shows two examples of LCs for which the least-squares algorithm has converged to solutions that reproduce the bulk features of the LCs quite well, yet exhibit a large F⁢2. Therefore, this must be due to inadequacies of the physical model, underestimated measurement uncertainties, or a mix of both. Shortcomings of the physical model may include ignoring intrinsic variability of the components or ignoring the presence of spots or circumstellar disks, but may also be related to an inferior numerical accuracy of the simulator output compared to the accuracy of Gaia photometry. At the same time, underestimated measurement uncertainties cannot be discounted as the calibration effort of Gaia photometry is still ongoing. These scenarios, along with possible remedies (such as adding jitter to the model fluxes when appropriate) are currently under investigation.

Figure 7.54: Folded eclipsing binary light curves, and their best-fit models. The Gaia data are shown with green dots; uncertainties are included but are usually smaller than the dot size. The magenta circles indicate the flux values predicted by the best-fit model at the same phases as the observations. The dotted blue line shows intermediate model fluxes. Black dots indicate data outliers, as identified by variability processing; these are ignored in the fitting procedure. The vertical dotted lines indicate the eclipse mid-points. The vertical dashed lines indicate the beginning and the end of the eclipses, and they are strictly valid for detached systems only. (a): The large F⁢2=32.36 value of the solution contrasts with the good visual impression of the best-fit model. The discrepancy could be caused by missing physics in the model (e.g., discarding spots), and/or by underestimated uncertainties in the photometry. (b): This solution is arguably visually worse than the one on (a), yet its F⁢2=23.73 value, though still large, is significantly lower. Most of the uncertainties remain invisibly small, but they are bigger relative to the signal than the uncertainties on (a), consistent with the fact that the signal is now 3-4 times weaker. The causes of the large F⁢2 value are likely the same as before; however, the fact that a significant increase in data point scatter is more than offset by an increase of the photometric uncertainties points to the latter as the largest contributor to F⁢2.

In the meantime, and as a way of facilitating filtering operations performed on the basis of the goodness of fit (such as in Section 7.6.5), the g_rank, presented in Section 7.6.5, offers the possibility of ranking LCs based solely on the flux values of their data points, unaffected by concerns about their uncertainties.

Reliability of parameter uncertainties

The quoted uncertainties for the fitted parameters come from the covariance matrix of the solution, as calculated by the Levenberg-Marquardt method. However, the off-diagonal elements of the covariance matrix are a measure of the pairwise correlations between parameters to first order only. More realistic uncertainties may be provided by MCMC simulations, but these were out of scope for Gaia DR3. This implies that the reported parameter uncertainties are likely generally underestimated. It should also be reminded that the calculation of the covariance matrix involves the computation of numerical derivatives which are sometimes of limited accuracy.

Furthermore, as discussed in Section 7.6.6, the F⁢2 of the solutions does not follow the normal distribution 𝒩⁢(0,1). The user should consider applying the correction suggested in Section 7.2.3, i.e., multiplying the parameter uncertainties by the coefficient given by Equation 7.4.

Uncertainty for 𝐭Z actually refers to 𝐭0

The time reference calculated by the local optimisation is t0, the time when the primary component is eclipsed by the secondary. However, as mentioned in Section 7.6.5, the published time reference is instead tZ, the time of periastron passage. However, the transformation from t0 to tZ was done only for the value of the parameter, and not for its uncertainty. In other words, the provided uncertainty still corresponds to that of t0. This oversight was discovered too late to be corrected for Gaia DR3.

Error in the calculation of mutual irradiation effects

Late in the validation process, it was discovered that a software bug in the mutual irradiation algorithm (cf. Section 7.6.3) disables the calculation of irradiation effects under certain conditions. This bug is expected to mostly affect solutions for systems characterised by a combination of large fill factors and a significant temperature difference.

Spurious non-circular systems for arguments of periastron close to 90∘ and 270∘

Figure 7.55: Density map of the argument of periastron as a function of eccentricity for the eclipsing binary solutions. The overdensities at higher eccentricities around ω≈90∘ and ω≈270∘ correspond to eccentric systems viewed along their semi-major axis. At least for detached binaries, the light curves of such systems are indistinguishable from circular systems, in the sense that the eclipses are half a period apart. Since the eccentricities of most of these systems are spurious, they were not included in Gaia DR3 when e>0.01 and ω∈[60∘,120∘]∪[240∘,300∘]. Note that this diagram may give a false impression about the relative number of eccentric systems, as most eclipsing binary solutions correspond to circular systems located at e=ω=0.

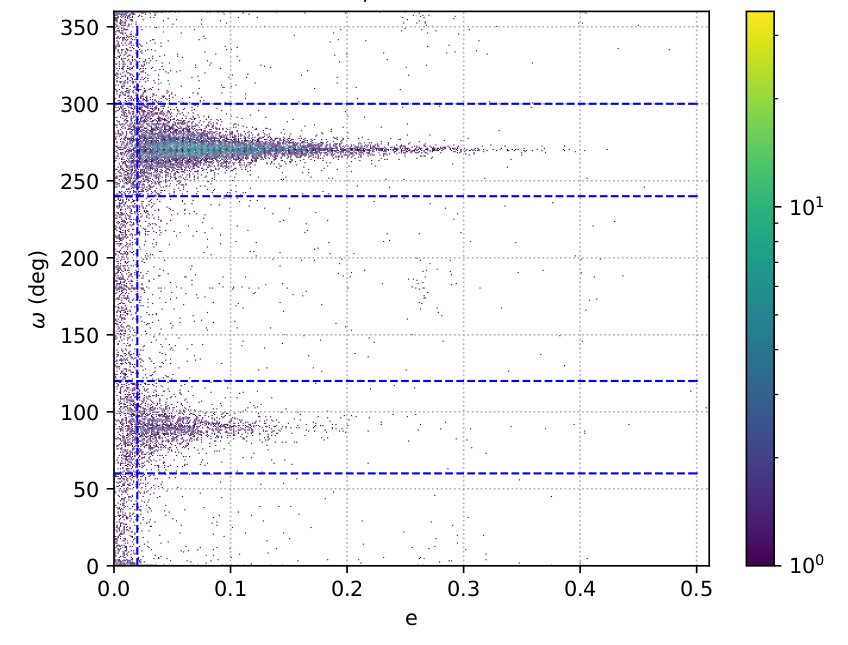
When an EB is viewed along its semimajor axis, i.e., when ω≈90∘ or ω≈270∘, it is not possible to determine from its LC whether it is circular or eccentric, especially in the case of a detached system. This is an inherent degeneracy of the problem that occurs because even if the system is eccentric, the eclipses still occur half a period apart. During local optimisation, nothing prevents the Levenberg-Marquardt algorithm from fitting a near-circular system with an eccentric system having an argument of periastron close to 90∘ or 270∘. This effect causes an excess of spurious eccentric solutions around these ω angles, as shown in Figure 7.55. In order to reduce the number of these spurious solutions, they were filtered out when e>0.01 and ω∈[60∘,120∘]∪[240∘,300∘]. However, it should be expected that a number of non-excluded solutions with e<0.01 around the affected ω regions are also, in reality, circular orbits. Although this degeneracy cannot be fully avoided, future data releases can attempt to mitigate it, for example by trying circular solutions near these ω angles, and by improving the performance of global optimisation.

Inclination angles exceeding 90∘

It is not possible to detect retrograde motion from EB LCs. Therefore, there is no meaning in reporting inclination values exceeding 90∘. However, in order to avoid having the interesting case of i≈90∘ mapped near the edge of the logit transformation that is used to constrain the local optimisation, i was left to vary up to 180∘. Unfortunately, by omission, its value was not mapped back to ≤90∘, so it is incumbent on the end user to perform this transformation.

Third light ignored

When a “third” source of light, usually a background or foreground star, is included in the photometry of an EB, it has the effect of rendering the eclipses more shallow, roughly emulating a system with a lower inclination. This effect should be more common with fainter EBs located in dense stellar fields. Although the EB simulator has the ability of fitting a third light, it was not enabled because it cannot be done robustly with a single-passband LC.

The period is not fitted

The period of photometric variability, and hence also the orbital period of the EB, is taken from variability processing, as mentioned in Section 7.6.2. Preliminary experiments to include the period as a free parameter in model fitting did not bring any improvement, at least in the context of the split global-local optimisation scheme currently employed. This also means that the uncertainty in the period is not taken into account when computing the covariance matrix of the solution (i.e., its influence on the uncertainties of other parameters is ignored).