3.3 Calibration models 3.3.5 Attitude model 3.3.7 Global parameters

3.3.6 Geometric instrument model

Author(s): Lennart Lindegren

Figure 3.12: Schematic illustration of the definition of observation lines in field angles.

The geometric instrument model (or astrometric calibration model) is an accurate description of the CCD layout in the Scanning Reference System (SRS; Section 3.1.3) $\mathsf{S}=[\boldsymbol{x}~{}\boldsymbol{y}~{}\boldsymbol{z}]$ , or equivalently in instrument angles $(\varphi,\zeta)$ or field angles $(f,\eta,\zeta)$ . The three systems are equivalent because a given direction $\boldsymbol{u}$ can be represented in either system by means of the relations

\mathsf{S}^{\prime}\boldsymbol{u}=\begin{bmatrix}u_{x}\\ u_{y}\\ u_{z}\end{bmatrix}=\begin{bmatrix}\cos\zeta\cos\varphi\\ \cos\zeta\sin\varphi\\ \sin\zeta\end{bmatrix}=\begin{bmatrix}\cos\zeta\cos(\eta+f\Gamma_{\text{c}})\\ \cos\zeta\sin(\eta+f\Gamma_{\text{c}})\\ \sin\zeta\end{bmatrix}

(3.115)

where $f=\text{sign}(u_{y})$ is the field index ( $f=+1$ in preceding field of view, $-1$ in following field of view) and $\Gamma_{\text{c}}=106\hbox{$.\!\!^{\circ}$}5$ is the conventional basic angle. Conversely, the $x y$ plane of the SRS and the origin of the along-scan (AL) instrument angle $\varphi$ are implicitly defined by the geometric instrument model, or more precisely by certain constraints imposed on the model. The geometrical instrument model is based on the calibration model described in Section 3.4 of Lindegren et al. (2012).

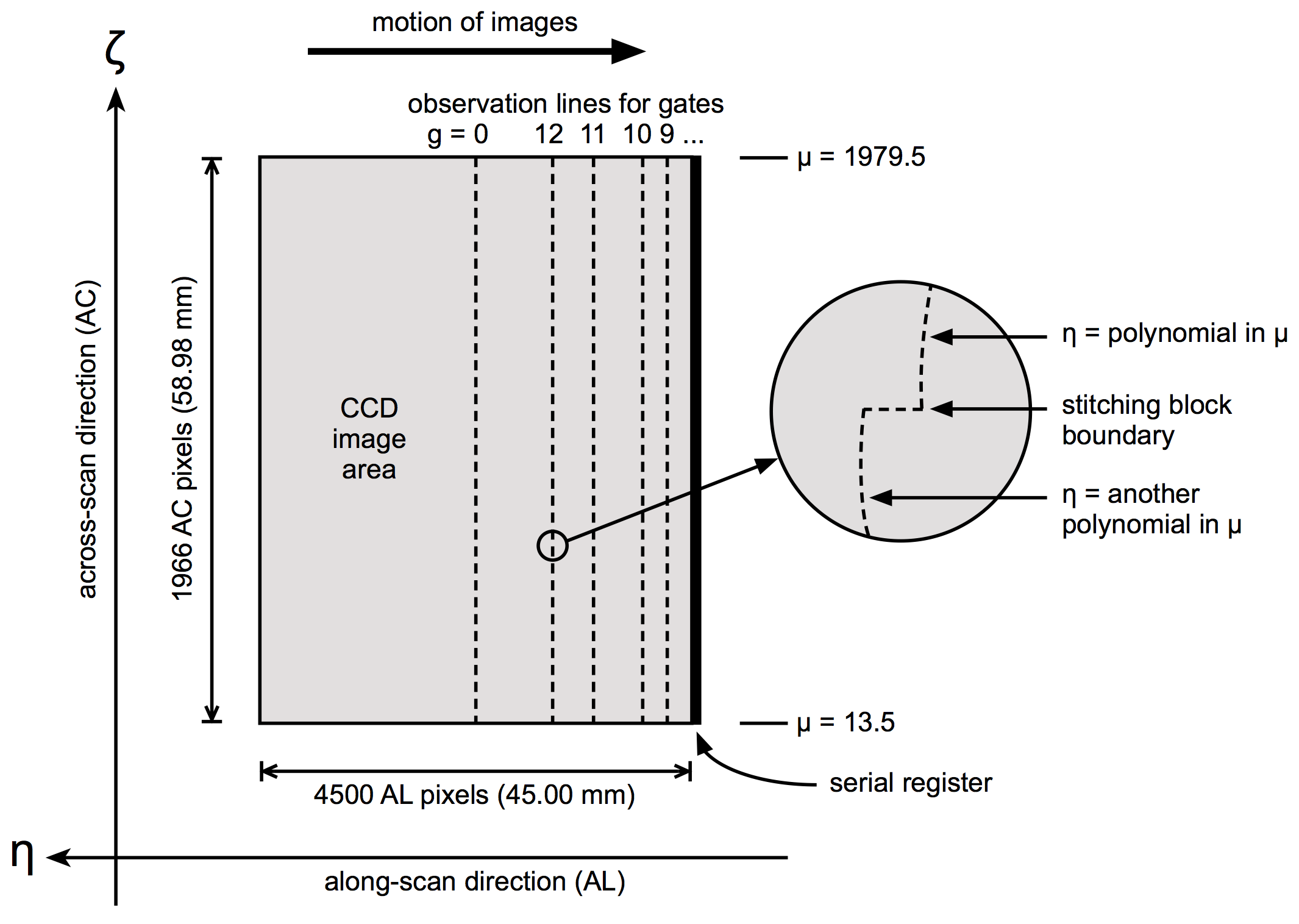
A central concept for the geometric instrument calibration is the observation line, which is an imaginary curve extending over the full width of the CCD image area in the across-scan (AC) direction (Figure 3.12). For ungated observations (gate index $g=0$ ), where all $\simeq\,$ 4500 AL pixels are used to integrate the image, the observation line is nominally situated $\simeq\,$ 2250 TDI lines prior to the serial register (see Table 3.4 for exact numbers). For gated observations using the first gate ( $g=12$ ), only the last $\simeq\,$ 2900 TDI lines are used for the integration, and the observation line is consequently situated $\simeq\,$ 1450 TDI lines prior to the serial register. The AC pixel coordinate $\mu$ is a continuous variable in the range $[13.5,\,1979.5]$ , with $\mu=14.0$ when the image is centrally located in the AC direction of the first pixel column (with the smallest AC field angle $\zeta$ ), and $\mu=1979.0$ when the image is centrally located in the AC direction of the last (1966th) pixel column.

The elementary astrometric measurement, obtained from the transit of a given source over a single (SM or AF) CCD, is the observation time $t_{\text{obs}}$ and AC pixel coordinate of the image, $\mu_{\text{obs}}$ . The observation time is calculated, in on-board time, as the read-out time of the reference pixel of the observation window, corrected for the AL offset of the image centroid from the reference pixel, minus the exposure mid-time offset for the relevant $g$ (Table 3.4). ( $t_{\text{obs}}$ is subsequently converted to TCB using the time ephemeris; see Section 3.1.3.) The observed AC pixel coordinate $\mu_{\text{obs}}$ is obtained by correcting the AC coordinate of the window reference pixel for the AC offset of the image centroid from the reference pixel, but is only available for observations using a two-dimensional window.

Table 3.4: Nominal characteristics of gated observations.

$g$	TDI lines used	Exposure time	Exposure mid-time offset
0	3,4,7,8,11:4500	4494	2253.497330
1*	3,4	2	3.500000
2*	3,4,7,8	4	5.500000
3*	3,4,7,8,11:14	8	9.000000
4	3,4,7,8,11:22	16	13.750000
5*	3,4,7,8,11:38	32	22.125000
6*	3,4,7,8,11:70	64	38.312500
7	3,4,7,8,11:134	128	70.406250
8	3,4,7,8,11:262	256	134.453125
9	3,4,7,8,11:518	512	262.476562
10	3,4,7,8,11:1030	1024	518.488281
11	3,4,7,8,11:2054	2048	1030.494141
12	3,4,7,8,11:2906	2900	1456.495862

Notes.

g

is the gate index (0 for un-gated observations, 1–12 for gated observations, with

g=1

used for the brightest stars). An asterisk indicates gates that are not used in normal operations. The second column lists the TDI lines used for a given gate, with the TDI lines numbered from 1 to 4500, counted from the serial register. Note that TDI lines 1, 2, 5, 6, 9, and 10 are permanently blocked for light. The exposure time, measured in TDI periods of exactly 0.9828 ms on-board time, is the total number of active TDI lines when a given gate is activated (or none activated if

g=0

). The notation 11:4500 means TDI lines 11 through 4500 (inclusive). The exposure mid-time offset is the mean value of the active TDI line numbers, and corresponds to the nominal location of the observation line, expressed as the number of TDI periods before the instant when the pixel content is in the serial register.

The optical design of the Gaia telescopes and the mechanical layout of the focal-plane assembly are such that the TDI lines of all the CCD are very nearly parallel to lines of constant AL field angle $\eta$ in the SRS. (This is a necessary condition for the TDI operation of all the CCDs using the same TDI period.) Thus, to a first approximation the observation lines are short segments of great-circle arcs with a fixed $\eta$ for a given CCD and gate. However, in reality the structure of an observation line is much more complex, as suggested by the ’magnifying glass’ in Figure 3.12. For a given CCD/gate combination, the observation lines are different in the two fields of view, due to the optical distortions being different, and they vary with time due to thermal-mechanical changes in the optics and focal-plane assembly. Additional dependences (e.g, on window class $w$ ) are discussed below.

The observation line for a given combination of field index $f$ , CCD index $n$ (e.g., in the range 1 through 62 in the AF), gate $g$ , and window class $w$ is defined in parametric form as

\left.\begin{aligned} \displaystyle\eta&\displaystyle=\eta_{fngw}(\mu,\,t,\,% \dots)\\ \displaystyle\zeta&\displaystyle=\zeta_{fngw}(\mu,\,t,\,\dots)\end{aligned}% \quad\right\}\,,\quad 13.5\leq\mu\leq 1979.5\,.

(3.116)

Index $w=0$ , 1, or 2 refers to the window class (or sampling class) assigned to the observation by the on-board processing software, based on the on-board estimate of the $G$ magnitude; see Section 1.1.3 and Table 1.1 for details. Note that only eight of the gate settings, corresponding to $g=0$ , 12, 11, 10, 9, 8, 7, and 4 (see Table 3.4) are used in nominal operations.

Since $\mu_{\text{obs}}$ is only available for observations in two-dimensional windows, the argument $\mu$ in Equation 3.116 should be the AC pixel coordinate of the image calculated from current source, attitude, and calibration parameters. The dependence on $\mu$ involves both large-scale effects, such as the slope and curvature of the observation line, medium-scale effects, for example caused by the stitch blocks, and small-scale effects that vary on a level of a few pixel columns or units in $\mu$ . The required precision in the calculated $\mu$ is therefore very modest ( $\sim\,$ 1 unit), and even a very preliminary set of parameters will be sufficient for this. However, for Gaia DR2 an approximate $\mu$ was instead calculated from the AC window coordinate provided by the IDU (Section 2.4.2).

The time argument $t$ in Equation 3.116 is the observation time $t_{\text{obs}}$ , which should here be understood as representing the slow variation of the observation lines with time, including for example the basic-angle variations — these are ‘slow’ (time scales of hours to years) in comparison with the precisions involved in measuring $t_{\text{obs}}$ , which are in the $\mu$ s range. The time dependence in Equation 3.116 must be able to accommodate both gradual and sudden changes of the instrument geometry. The former could for example be caused by ageing of the mechanical structure, variations in the thermal environment, and the progressive development of change transfer inefficiency in the CCD detectors. Sudden changes may happen spontaneously or in connection with planned operational events such as mirror decontaminations, telescope refocusing, and special calibration activities. The existence of sudden changes, whether they are planned or spontaneous, makes it necessary to have breakpoints (discontinuities) in the geometric model at specific times. The times of discontinuities are known for planned events but are in other cases only found by inspection of the actual data.

The time dependence is generally modelled by dividing the full time interval $[t_{0},t_{J}]$ covered by the instrument model into a set of $J$ contiguous time granules, such that the granule indexed by $j$ ( $j=0\dots J-1$ ) covers $t_{j}<t<j_{j+1}$ . Here, $t_{j}$ ( $j=0\dots J$ ) are the chosen breakpoints, with $t_{0}$ and $t_{J}$ at the beginning and end of the full time interval covered by the model. Within a granule the variation is modelled as a low-order polynomial. To ensure that the polynomial model is accurate enough within a granule, it may be necessary to insert additional breakpoints — not motivated by known discontinuities in the data — at suitable times to limit the size of the granules. Continuity conditions are never imposed across breakpoints.

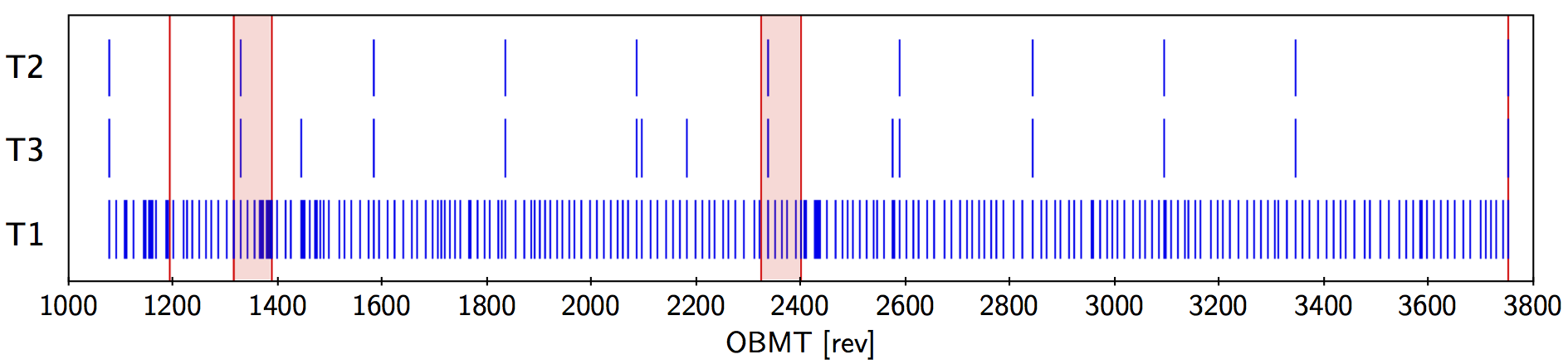
Different effects may require different time resolutions. Generally speaking, small-scale effects, representing mainly the internal structure of the CCDs, are stable over long times, while large-scale effects, depending on opto-mechanical variations, tend to vary significantly on much shorter time scales. The geometric instrument model uses several different time axes, each with its own granularity, or set of breakpoints. For practical reasons the time axes should be hierarchic in the sense that the breakpoints of a coarser time axis is a subset of the breakpoints of the finer time axis. For Gaia DR2 three time axes are used: T1 with 243 granules, T2 with 10 granules, and T3 with 14 granules (Figure 3.13). T1 is used for the rapidly changing large-scale distortion, while T2 and T3 are used for less critical or more slowly evolving effects.

Figure 3.13: Time axes T1, T2, T3 used for the geometric instrument model in Gaia DR2. The vertical blue lines mark the breakpoints. The first and last red lines mark the beginning and end of the time interval used in the primary astrometric solution and for all astrometric results. The pink intervals are the gaps during and after decontaminations.

The dots ( $\dots$ ) in Equation 3.116 represent possible dependences on additional continuous variables such as the colour and magnitude of the source at the time of observation (COMA terms; see Section 3.3.6).

The functions in Equation 3.116 are written as sums of a fixed reference calibration $\eta_{ng}^{(0)}(\mu)$ , $\zeta_{ng}^{(0)}(\mu)$ , calculated from the nominal layout of the CCDs and gates, and a number of ‘effects’, which in turn are linear combinations of basis functions with the calibration parameters as coefficients. The generic expressions are

\left.\begin{aligned} \displaystyle\eta_{fngw}(\mu,t,\dots)&\displaystyle=\eta% _{ng}^{(0)}(\mu)+\sum_{r}E^{\text{AL}}_{r}(o)\\ \displaystyle\zeta_{fngw}(\mu,t,\dots)&\displaystyle=\zeta_{ng}^{(0)}(\mu)+% \sum_{r}E^{\text{AC}}_{r}(o)\end{aligned}\quad\right\}\,,

(3.117)

where $E^{\text{AL}}_{r}$ and $E^{\text{AC}}_{r}$ are the AL and AC calibration effects detailed in Section 3.3.6 and Section 3.3.6. The effects are here formally written as functions of the observation index $o$ , from which all other required indices and arguments can be obtained (Figure 3.14).

Figure 3.14: Quantities derived from the observation index $o$ .

The AL and AC calibration parameters for effect $r$ are in the following designated $\Delta\eta_{X}^{(r)}$ and $\Delta\zeta_{Y}^{(r)}$ , where $X$ and $Y$ stand for any relevant combination of indices needed to uniquely identify the corresponding basis function $\Phi$ ; thus

\left.\begin{aligned} \displaystyle E^{\text{AL}}_{r}(o)&\displaystyle=\sum_{X% }\Delta\eta_{X}^{(r)}\Phi_{X}^{(r)}(o)\\ \displaystyle E^{\text{AC}}_{r}(o)&\displaystyle=\sum_{Y}\Delta\zeta_{Y}^{(r)}% \Phi_{Y}^{(r)}(o)\end{aligned}\quad\right\}\,.

(3.118)

$X$ and $Y$ may include any subset of the indices $f$ (field-of-view index), $n$ (CCD index), $g$ (gate), $w$ (window class), $j$ (granule index for the relevant time axis), and the additional indices $b$ , $l$ , and $m$ defined below. $b$ is the stitch-block index calculated as

b=\lfloor(\mu+128.5)/250\rfloor\,.

(3.119)

$l$ and $m$ are indices used to distinguish basis functions that describe the dependences of $\mu$ (within a given CCD $n$ ) and $t$ (within a given granule $j$ ). The order of indices in $X$ and $Y$ is taken to be $l m j f n g b w$ .

The adopted basis functions for the dependences on $\mu$ and $t$ are shifted Legendre polynomials $\tilde{P}_{n}(x)=P_{n}(2x-1)$ , where $P_{n}(x)$ are the normal (non-shifted) Legendre polynomials. The shifted Legendre polynomials are orthogonal on $[0,\,1]$ and reach $\pm 1$ at the end points. The first four polynomials are

\left.\begin{aligned} \displaystyle\tilde{P}_{0}(x)&\displaystyle=1\\ \displaystyle\tilde{P}_{1}(x)&\displaystyle=2x-1\\ \displaystyle\tilde{P}_{2}(x)&\displaystyle=6x^{2}-6x+1\\ \displaystyle\tilde{P}_{3}(x)&\displaystyle=20x^{3}-30x^{2}+12x-1\end{aligned}% \quad\right\}\,.

(3.120)

The joint dependence on $\mu$ and $t$ can be written as linear combinations of basis functions that are products of the shifted Legendre polynomials of degree $l$ and $m$ , i.e.

\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(\tilde{t}\,)\,,

(3.121)

where

\tilde{\mu}=\frac{\mu-\mu_{\text{min}}}{\mu_{\text{max}}-\mu_{\text{min}}}

(3.122)

is the normalised AC pixel coordinate, with the limits $\mu_{\text{min}}=13.5$ and $\mu_{\text{max}}=1979.5$ (Figure 3.12), and

\tilde{t}=\frac{t-t_{j}}{t_{j+1}-t_{j}}

(3.123)

the normalised time within granule $j$ , with $t_{j}\leq t<t_{j+1}$ .

The calibration requirements are much stricter AL than AC, and the models for $\eta_{fngw}(\mu,\,t,\,\dots)$ and $\zeta_{fngw}(\mu,\,t,\,\dots)$ are separately described hereafter. The particular models described here are the ones used for Gaia DR2 (see Section 3.3 in Lindegren et al. 2018); more elaborate models will be used for subsequent releases.

AL geometric instrument model

The AL geometric instrument model is the sum of the five effects enumerated below.

AL large scale ( $r=1$ ) describes the relatively rapid variations of the large-scale distortion, and therefore uses the time axis T1 with the smallest granules (typically 3 days). It depends on the field and CCD indices, but is the same for all gates, blocks, and window classes. It assumes a quadratic dependence on $\mu$ and a linear dependence on $t$ within a granule, and is therefore a linear combination of four basis functions,

\begin{split}\displaystyle E^{\text{AL}}_{1}(o)&\displaystyle=\sum_{lm\,=\,00,% \,10,\,20,\,01}\Delta\eta^{(1)}_{lmjfn}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}% (\tilde{t})\\ &\displaystyle=\Delta\eta^{(1)}_{00jfn}+\Delta\eta^{(1)}_{10jfn}\tilde{P}_{1}(% \tilde{\mu})+\Delta\eta^{(1)}_{20jfn}\tilde{P}_{2}(\tilde{\mu})+\Delta\eta^{(1% )}_{01jfn}\tilde{P}_{1}(\tilde{t})\,,\end{split}

(3.124)

with a total of $4\times 243\times 2\times 62=120\,528$ calibration parameters.

2.

AL medium scale, gate ( $r=2$ ) describes the slowly varying joint dependence on gate ( $g$ ) and stitch block ( $b$ ). The times axis is T2 with granules of typically 63 days. The model assumes a linear dependence on $\mu$ for each gate/block combination, and no time variation within a granule. The effect is therefore a linear combination of two basis functions,

$\begin{split}\displaystyle E^{\text{AL}}_{2}(o)&\displaystyle=\sum_{lm\,=\,00,% \,10}\Delta\eta^{(2)}_{lmjfngb}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(\tilde{% t})\\ &\displaystyle=\Delta\eta^{(2)}_{00jfngb}+\Delta\eta^{(2)}_{10jfngb}\tilde{P}_% {1}(\tilde{\mu})\,,\end{split}$ (3.125)

with a total of $2\times 10\times 2\times 62\times 8\times 9=178\,560$ calibration parameters.
3.

AL large scale, window class ( $r=3$ ) describes the slowly varying dependence on window class ( $w$ ), using times axis is T3 with granules of typically 63 days. The model assumes a linear dependence on $\mu$ for each window class, and no time variation within a granule. The effect is therefore a linear combination of two basis functions,

$\begin{split}\displaystyle E^{\text{AL}}_{3}(o)&\displaystyle=\sum_{lm\,=\,00,% \,10}\Delta\eta^{(3)}_{lmjfnw}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(\tilde{t% })\\ &\displaystyle=\Delta\eta^{(3)}_{00jfnw}+\Delta\eta^{(3)}_{10jfnw}\tilde{P}_{1% }(\tilde{\mu})\,,\end{split}$ (3.126)

with a total of $2\times 14\times 2\times 62\times 3=10\,416$ calibration parameters.

AL large scale, colour ( $r=4$ ) describes the AL chromaticity of the geometric instrument model. The chromaticity is found to be different depending on the window class, and the effect is therefore modelled similarly to $E^{\text{AL}}_{3}(o)$ except that it has a linear dependence on $\nu_{\text{eff}}$ (Section 3.3.4). Moreover, to account for the more rapidly developing chromaticity the model allows a linear variation with time within a granule. The effect is a linear combination of three basis functions,

\begin{split}\displaystyle E^{\text{AL}}_{4}(o)=&\displaystyle\sum_{lm\,=\,00,% \,10,\,01}\Delta\eta^{(4)}_{lmjfnw}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(% \tilde{t})\,(\nu_{\text{eff}}-\nu_{\text{eff}}^{\text{ref}})\\ \displaystyle=&\displaystyle\Delta\eta^{(4)}_{00jfnw}(\nu_{\text{eff}}-\nu_{% \text{eff}}^{\text{ref}})+\Delta\eta^{(4)}_{10jfnw}\tilde{P}_{1}(\tilde{\mu})% \,(\nu_{\text{eff}}-\nu_{\text{eff}}^{\text{ref}})\\ &\displaystyle+\Delta\eta^{(4)}_{01jfnw}\tilde{P}_{1}(\tilde{t})\,(\nu_{\text{% eff}}-\nu_{\text{eff}}^{\text{ref}})\,,\end{split}

(3.127)

where $\nu_{\text{ff}}^{\text{ref}}=1.6~{}\mu\text{m}^{-1}$ is the reference value of the effective wavenumber. This effect has a total of $3\times 14\times 2\times 62\times 3=15\,624$ calibration parameters.

AL large scale, magnitude ( $r=5$ ) describes the magnitude-dependence of the geometric instrument model. Similarly to the chromaticity is found to depending on the window class, and the effect is therefore modelled similarly to $E^{\text{AL}}_{3}(o)$ except that it has a linear dependence on $G$ . The effect is a linear combination of two basis functions,

\begin{split}\displaystyle E^{\text{AL}}_{5}(o)&\displaystyle=\sum_{lm\,=\,00,% \,10}\Delta\eta^{(5)}_{lmjfnw}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(\tilde{t% })\,(G-G^{\text{ref}})\\ &\displaystyle=\Delta\eta^{(5)}_{00jfnw}(G-G^{\text{ref}})+\Delta\eta^{(5)}_{1% 0jfnw}\tilde{P}_{1}(\tilde{\mu})\,(G-G^{\text{ref}})\,,\end{split}

(3.128)

where $G^{\text{ref}}=13$ mag is the reference magnitude. This effect has a total of $2\times 14\times 2\times 62\times 3=10\,416$ calibration parameters.

Counting all five effects, the number of AL calibration parameters is 335 544. Some of them refer to time granules not used in the primary solution (Figure 3.13); they are however all estimated in the AGIS post-processing in order to provide calibration data with maximum time coverage for other processes such as the photometry.

AC geometric instrument model

The AC geometric instrument model is similar to the AL model, except that time axis T3 with a typical granule size of 63 days is used for all the effects, that the gate effect has no dependence on $\mu$ , and that there is no dependence on the stitch block index $b$ . The model is the sum of the five effects enumerated below.

AC large scale ( $r=1$ ) describes the variations of the large-scale distortion, using time axis T3. It depends on the field and CCD indices, but is the same for all gates, blocks, and window classes. It assumes a quadratic dependence on $\mu$ and a linear dependence on $t$ within a granule, and is therefore a linear combination of four basis functions,

\begin{split}\displaystyle E^{\text{AC}}_{1}(o)&\displaystyle=\sum_{lm\,=\,00,% \,10,\,20,\,01}\Delta\zeta^{(1)}_{lmjfn}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m% }(\tilde{t})\\ &\displaystyle=\Delta\zeta^{(1)}_{00jfn}+\Delta\zeta^{(1)}_{10jfn}\tilde{P}_{1% }(\tilde{\mu})+\Delta\zeta^{(1)}_{20jfn}\tilde{P}_{2}(\tilde{\mu})+\Delta\zeta% ^{(1)}_{01jfn}\tilde{P}_{1}(\tilde{t})\,,\end{split}

(3.129)

with a total of $4\times 14\times 2\times 62=6\,944$ calibration parameters.

2.

AC medium scale, gate ( $r=2$ ) describes the dependence on gate ( $g$ ), using times axis T3. The model assumes a constant offset for each gate, and no time variation within a granule. The effect is therefore

$\begin{split}\displaystyle E^{\text{AC}}_{2}(o)&\displaystyle=\sum_{lm\,=\,00}% \Delta\zeta^{(2)}_{lmjfng}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(\tilde{t})\\ &\displaystyle=\Delta\zeta^{(2)}_{00jfng}\,,\end{split}$ (3.130)

with a total of $1\times 14\times 2\times 62\times 8=13\,888$ calibration parameters.
3.

AC large scale, window class ( $r=3$ ) describes the dependence on window class ( $w$ ), using times axis is T3. The model assumes a linear dependence on $\mu$ for each window class, and no time variation within a granule. The effect is therefore a linear combination of two basis functions,

$\begin{split}\displaystyle E^{\text{AC}}_{3}(o)&\displaystyle=\sum_{lm\,=\,00,% \,10}\Delta\zeta^{(3)}_{lmjfnw}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(\tilde{% t})\\ &\displaystyle=\Delta\zeta^{(3)}_{00jfnw}+\Delta\zeta^{(3)}_{10jfnw}\tilde{P}_% {1}(\tilde{\mu})\,,\end{split}$ (3.131)

with a total of $2\times 14\times 2\times 62\times 3=10\,416$ calibration parameters.

AC large scale, colour ( $r=4$ ) describes the AC chromaticity of the geometric instrument model. The effect is a linear combination of three basis functions,

\begin{split}\displaystyle E^{\text{AC}}_{4}(o)=&\displaystyle\sum_{lm\,=\,00,% \,10,\,01}\Delta\zeta^{(4)}_{lmjfnw}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(% \tilde{t})\,(\nu_{\text{eff}}-\nu_{\text{eff}}^{\text{ref}})\\ \displaystyle=&\displaystyle\Delta\zeta^{(4)}_{00jfnw}(\nu_{\text{eff}}-\nu_{% \text{eff}}^{\text{ref}})+\Delta\zeta^{(4)}_{10jfnw}\tilde{P}_{1}(\tilde{\mu})% \,(\nu_{\text{eff}}-\nu_{\text{eff}}^{\text{ref}})\\ &\displaystyle+\Delta\zeta^{(4)}_{01jfnw}\tilde{P}_{1}(\tilde{t})\,(\nu_{\text% {eff}}-\nu_{\text{eff}}^{\text{ref}})\,,\end{split}

(3.132)

AC large scale, magnitude ( $r=5$ ) describes the magnitude-dependence of the AC geometric instrument model. The effect is a linear combination of two basis functions,

\begin{split}\displaystyle E^{\text{AC}}_{5}(o)&\displaystyle=\sum_{lm\,=\,00,% \,10}\Delta\zeta^{(5)}_{lmjfnw}\tilde{P}_{l}(\tilde{\mu})\tilde{P}_{m}(\tilde{% t})\,(G-G^{\text{ref}})\\ &\displaystyle=\Delta\zeta^{(5)}_{00jfnw}(G-G^{\text{ref}})+\Delta\zeta^{(5)}_% {10jfnw}\tilde{P}_{1}(\tilde{\mu})\,(G-G^{\text{ref}})\,,\end{split}

(3.133)

where $G^{\text{ref}}=13$ mag is the reference magnitude. This effect has a total of $2\times 14\times 2\times 62\times 3=10\,416$ calibration parameters.

In total there are 57 288 AC calibration parameters.

Constraints

In the astrometric solution for Gaia, constraints may be used to eliminate degeneracies among the various kinds of parameters: source (S), attitude (A), calibration (C), and global (G) parameters. Such constraints are introduced solely in order to make the parameters (or subsets of them) uniquely determinable, but they will never in any way ‘force’ the solution against the data.

To clarify exactly what this means, consider that the astrometric solution essentially solves a weighted least-squares solution by minimising some quantity $Q(\boldsymbol{x})$ for the given data. Here $\boldsymbol{x}$ is the vector of all the parameters or unknowns. A valid solution $\boldsymbol{\hat{x}}$ is such that $Q(\boldsymbol{\hat{x}})\leq Q(\boldsymbol{x})$ for all $\boldsymbol{x}$ . (Here we assume that the problem is linear, i.e. we take $\boldsymbol{x}$ to be the correction to a preliminary estimate of the parameters, and consider only a limited region in solution space where $\eta$ and $\zeta$ vary linearly with $\boldsymbol{x}$ .) If $\boldsymbol{\hat{x}}$ is a valid solution and there exists a non-zero vector $\boldsymbol{v}$ such that $\boldsymbol{\hat{x}}+\alpha\boldsymbol{v}$ is also a valid solution for any scalar $\alpha$ , then the problem is degenerate with respect to $\boldsymbol{v}$ , and $\boldsymbol{v}$ is a null vector of the problem. The degeneracy can be removed by applying a constraint of the form $\boldsymbol{v}^{\prime}\boldsymbol{x}=0$ , which is equivalent to selecting the particular solution with $\alpha=-(\boldsymbol{v}^{\prime}\boldsymbol{\hat{x}})/(\boldsymbol{v}^{\prime}% \boldsymbol{v})$ . Since this is still a valid solution, the constraint does not increase $Q$ , i.e. it does not work against the data.

A well-known example of degeneracy in the astrometric solution concerns the celestial reference frame (Section 3.3.2). If the positions of all sources are changed by a solid rotation of the reference frame by some (small) angle around an arbitrary direction, and the attitude parameters are correspondingly changed, the modified source and attitude parameters will fit the data equally well as the original values. In this example only the source and attitude parameters are modified, while the calibration and global parameters are not changed. The degeneracy can therefore be described as a source–attitude (SA) degeneracy. It is removed by the frame rotator implementing constraints based on external information on quasars.

Other kinds of degeneracies involve other subsets of the parameters, e.g. calibration–attitude (CA), calibration–source (CS) and calibration–calibration (CC) degeneracies. Obviously only degeneracies involving the source parameters directly affect the astrometric results, while others (for example CA and CC) may affect the convergence of the iterative solution. To map the full spectrum of degeneracies relevant for a given set of models is a very complex problem that has not yet been satisfactorily solved.

For Gaia DR2 the only constraints enforced by the calibration update of the AGIS solution are the basic constraints

\sum_{f}\sum_{n}\Delta\eta^{(1)}_{00jfn}=0

(3.134)

for every $j$ , and

\sum_{n}\Delta\zeta^{(1)}_{00jfn}=0

(3.135)

for every combination of $j$ and $f$ . Roughly speaking, the mean displacement of the observation lines in the AL direction from their nominal locations should be zero at all times, when averaged over both fields of view and the 62 CCDs of the AF. Similarly, the mean displacement in the AC direction from the nominal locations should be zero at all times, when averaged over the 62 CCDs of the AF. This latter condition must be separately satisfied in each field of view in order to define the $x y$ plane of the SRS. In the absence of effects 2 and 3, these constraints would have been sufficient to define the origin of the field angles $(\eta,\,\zeta)$ and hence the SRS system (Section 3.1.1), effectively by ensuring a unique division between between the calibration and attitude parameters. The constraints Equation 3.134 and Equation 3.135 are therefore of the CA kind.

Unfortunately, AL and AC effects 2 and 3, as formulated in the preceding sections, require extra constraints to uphold a unique division between the calibration and attitude parameters. These additional CA constraints were not applied in the actual AGIS solutions for Gaia DR2. The resulting singularity of the least-squares system of equations was handled internally by the iterative solution algorithm, which effectively returns an arbitrary valid solution. Although this is unsatisfactory from several points of view, and should be improved in future releases, it should be noted that the missing CA constraints have a negligible impact on the astrometry as they do not directly involve the source parameters.

Degeneracies of the calibration–source (CS) kind are possible in the presence of the colour and magnitude effects 4 and 5, and could result in a reference frame where the orientation and spin ( $\boldsymbol{\varepsilon}_{0}$ and $\boldsymbol{\omega}$ ; see Section 3.3.2) have a linear dependence in $\nu_{\text{eff}}$ and $G$ . Since these effects depend on the window class, the colour and magnitude dependence of the reference frame could be different for sources predominantly observed in different window classes, e.g. for sources brighter and fainter than $G\simeq 13$ mag. As discussed in Lindegren et al. (2018) there are in fact clear signs of such effects in the Gaia DR2 proper motions at the level of $\sim\,$ 0.15 mas yr ${}^{-1}$ . The impact of such degeneracies on the astrometric results cannot be completely removed by means of constraints, but it is mitigated by the current use of time axis T3 for these effects, with a basic granularity of 63 days tuned to the precession period of the nominal scanning law (5.8 periods per year; Section 1.1.4).

COMA terms

The geometric instrument model described in Section 3.3.6 and Section 3.3.6 contains terms depending on colour ( $\nu_{\text{eff}}$ ) and magnitude ( $G$ ) through effects 4 and 5, the so-called COMA terms. They are needed because the location and shape of a point-source image, as seen by Gaia, in general depend on the colour of the object (e.g. due to wavelength-dependent diffraction effects in the optics) and its magnitude (e.g. due to charge transfer inefficiency in the CCD, which depends on the flux level). As described in Section 3.4.6, the intention is that COMA terms should eventually not be needed in the astrometric solution, namely when these effects are fully accounted for in the LSF and PSF calibrations. While this is not necessary for the processing of simple objects such as single stars, it will greatly simplify the (future) processing of more complex objects, and the purpose of this section is to explain the rationale for the adopted strategy. For simplicity the subsequent discussion focuses on the chromatic terms, although similar considerations apply to the magnitude effects.

Figure 3.15: Observation lines in local plane coordinates (LPC). (a) A point source S without proper motion or parallax is observed in three scans, with observation times $t_{\text{obs,1}}$ , $t_{\text{obs,2}}$ , $t_{\text{obs,3}}$ . (b) The observation lines projected onto the LPC $(a,\,d)$ produce three lines that intersect at P, the position of S in the LPC.

Procedures for analysing complex objects such as resolved, partially resolved, and astrometric binaries are not described in this documentation, as they will only be used for later releases. To allow a flexible approach to the modelling of such objects, it is however planned that their geometry will be described using local plane coordinates (LPC). These are rectangular coordinates $(a,\,d)$ in the tangent plane of the sky, with origin at some fixed reference point $(\alpha_{0},\delta_{0})$ , chosen for each object, and with the $a$ , $d$ axes pointing respectively towards increasing $\alpha$ and $\delta$ . The LPC are linear within a few arcsec of the reference position, which simplifies the modelling of complex motions such as a combination of proper motion, parallax, and binary orbital motion.

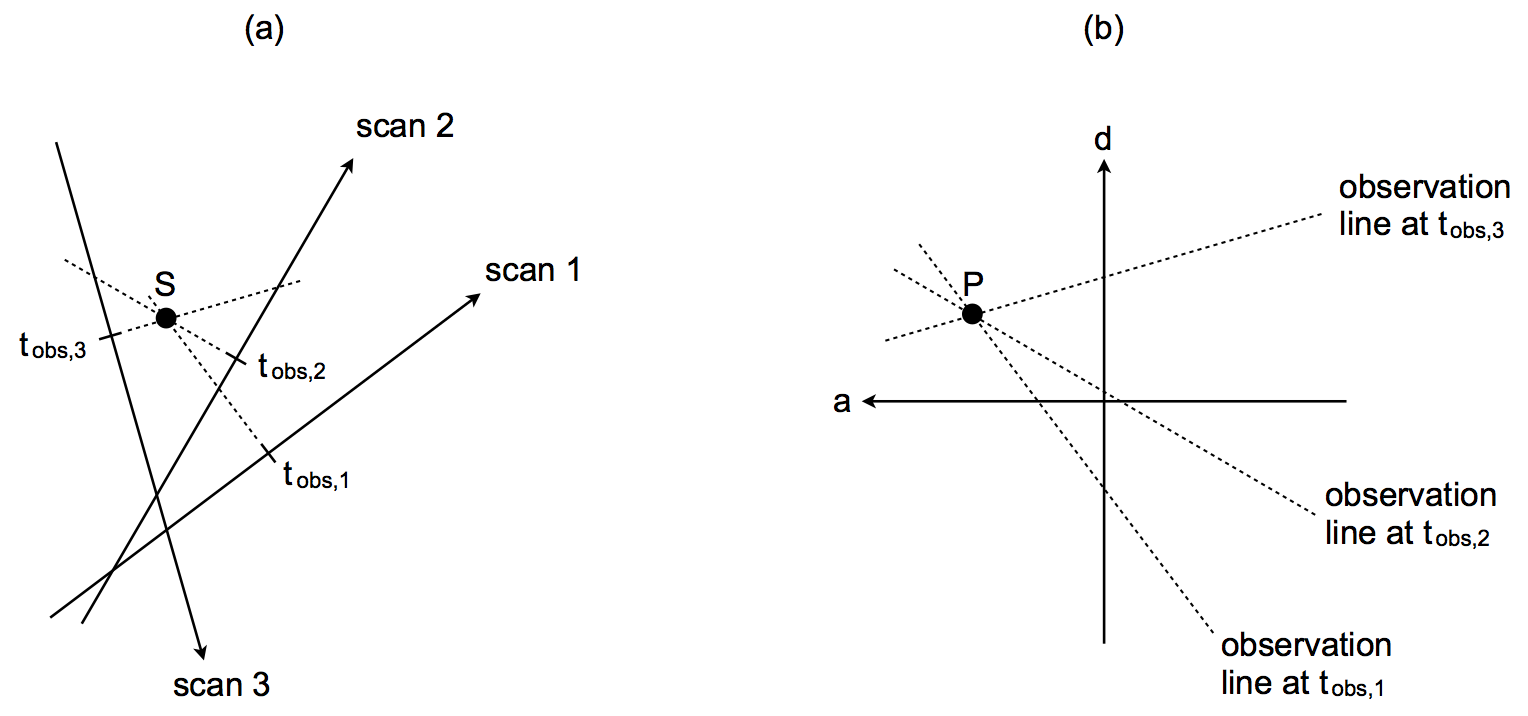
Recall that the geometric instrument model in Equation 3.116 is a parametric description of the ‘observation line’ in field angles $(\eta,\zeta)$ . Let $t_{\text{obs}}$ be the time when the image of a point source crosses this observation line with a known set of indices $f$ , $n$ , $g$ , and $w$ . Using the field index and the known attitude at $t_{\text{obs}}$ , it is possible to calculate the projection of the observation line onto the $(a,\,d)$ plane. In the absence of observational errors the actual point source must obviously be located somewhere along this line in LPC coordinates (Figure 3.15).

The presence of COMA terms in the geometric instrument model complicates this simple picture. The projection of the observation line in LPC is no longer unique, but depends on the assumed colour or the source. This is not a big problem as long as the object consists of a single point source with a known colour: including the COMA terms when computing the projections should still define a unique position. However, we also want to use the LPC for more complex objects, for example a partially resolved binary with components of different colours. We then need to compute the location in $(a,\,d)$ of each observed CCD sample $N_{k}$ (cf. Equation 2.2), using the time $t_{k}$ of the sample and the attitude and calibration data. But which colour should be used for the individual samples, if the calibration has non-zero COMA terms? Because of the overlapping LSF of the two sources, a sample does not uniquely belong to one or the other component, and therefore has no well-defined colour.

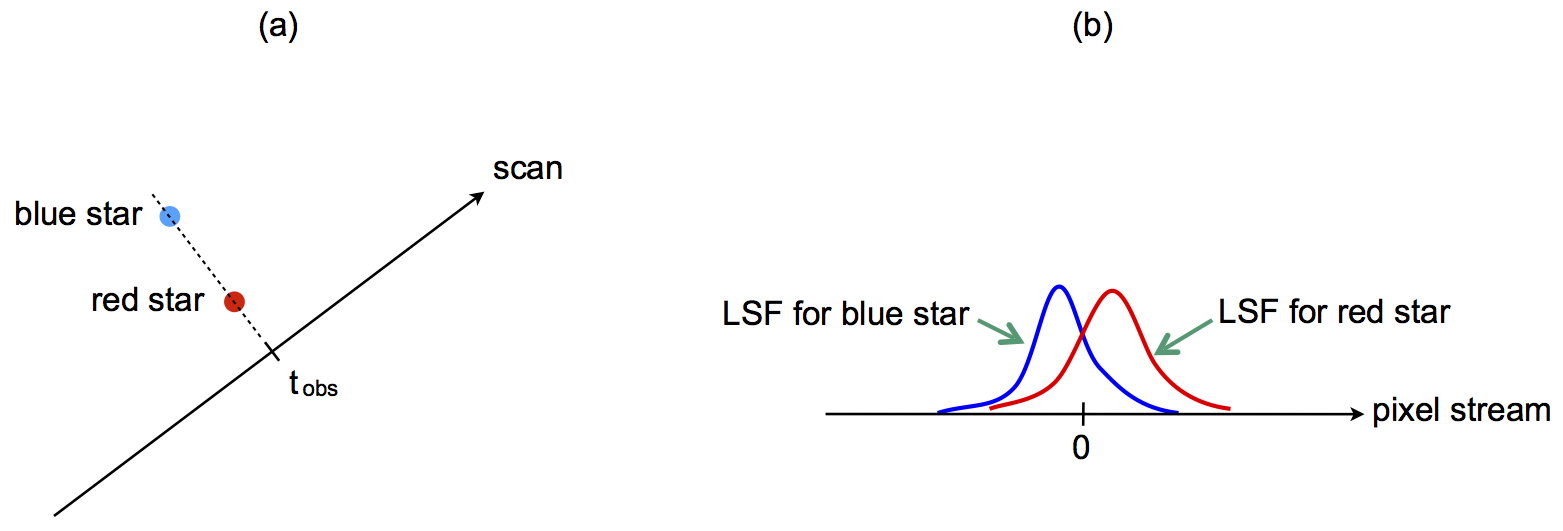
Figure 3.16: Chromaticity and the locations of the images of a blue and red star in the the pixel stream. (a) A binary consisting of a blue and a red star is scanned in a direction perpendicular to the arc connecting the stars. Conceptually, the observation time $t_{\text{obs}}$ should be the same for both components. (b) The image profiles (LSF) generated by the components are different due to the chromaticity of the instrument. However, if the origin of the LSF is achromatic, the two profiles have the same origin ‘0’, and the locations returned by the image parameter determination will also be the same. This will facilitate the analysis of the system in (a).

The conceptually simplest solution to this difficulty is to ensure that the origin of the LSF is achromatic, i.e. independent of colour. The meaning of this is illustrated in Figure 3.16. The chromatic terms in the geometric instrument model should then be strictly zero. Similarly, one must ensure that the origin of the LSF is independent of $G$ , in which case the magnitude-dependent terms of the geometric instrument model are zero.

These conditions are not met in the first few cycles of the Gaia data processing, in particular for Gaia DR1 and Gaia DR2. The geometric instrument model must therefore include COMA terms which in general are non-zero. An example is shown in Figure 3.19. In subsequent cycles the COMA terms should eventually vanish as the colour- and magnitude dependent effects become part of the PSF and LSF calibrations. Complete elimination of these effects by means of the PSF/LSF calibration will require several iterations of the cyclic processing loop. Even then, the COMA terms may however be retained in the astrometric solution for diagnostic purposes.

To achieve a colour- and magnitude-independent origin of the calibrated PSF and LSF, one needs the expected location of an image in the absence of COMA effects, precisely in order to include these effects in the PSF/LSF calibration. In the AGIS-PhotPipe-IDU iteration loop (Section 3.4.6), when the calibration parameters from the AGIS solution are fed back to the Intermediate Data Update (IDU), the COMA terms must therefore be set to zero.

European Space Agency

Science & Technology

3.3.6 Geometric instrument model

AL geometric instrument model

AC geometric instrument model

Constraints

COMA terms

Copyright 2024 © European Space Agency. All rights reserved.