4.4.7 Cross-match for the ICRS frame

Author(s): Jorge Fernández-Hernández, Hassan Siddiqui, Enrique Utrilla

As mentioned in Section 4.3.2, in order to align the Gaia reference frame, the optical counterparts of objects in the ICRF catalogue must be identified. This task was performed with a generic cross-matching tool. When no other features (e.g., colours, magnitudes, etc..) are considered we speak of spatial or positional cross-matching. This spatial identification is not easy. Due to different errors, instrument sensitivities and other characteristics of the data acquisition and calibration process, the same object may have slightly different coordinates in different catalogues.

These cross-matches usually involve millions or billions of objects that requires a much higher effort in the design of an efficient algorithm. At a first glance, this problem seems relatively straightforward: all we need is to compute the distance between every pair of points, and then choose the closest. The first naive solution leads to very long computation times for large numbers of points and for $N$ points, the computation time is $O(N^2)$. In an astronomical context, when the number of objects is large, this can quickly lead to problems (see Ivezić et al. (2014)). Therefore, making use of a spatial indexing is a fundamental component in any cross-match aiming to provide a good performance.

The cross-match described here is based on the simplest matching approach know as the ‘closest match’, which depend on positions only, and is considered adequate only when the positional uncertainties at the common epoch of the matched catalogues are all very small (see for example Wu et al. (2005)).

The cross-match algorithm provides the transformation of the source parameters from one initial epoch T0 to the arbitrary epoch T. Nevertheless, for this particular case, no epoch propagation was performed since the proper motions of the quasars used as reference are assumed to be zero.

Given the size of a typical astronomical catalogue (a few ${10}^8$-${10}^9$ sources) brute force cross-match would be computationally very expensive. Therefore, the input catalogues are partitioned making use of the HEALPix index. The following are the main steps followed by the cross-match:

1. 1.

   The reference catalogue is pre-arranged in a set of files associated with different HEALPix indexes to optimise the search.

2. 2.

   For a given external catalogue the system reads each source, extracting the required astronomical element to complete the cross-match. At the same time the application calculates its associated HEALPix value and the local files that would contain the reference sources to be cross-matched with. In order to do this, the boundaries of the HEALPix partition are checked to determine whether neighbouring HEALPix cells are overlapping with the cone search area.

3. 3.

   The contents of each of the selected HEALPix cells in the reference catalogue are loaded into memory. In order to improve performance a caching mechanism is used to minimise disk I/O.

4. 4.

   The angular distance between the external source and each of the selected reference sources is calculated using the haversine equation:

   $$d=2r\arcsin \left(\sqrt{{\sin }^2\left(\frac{{\phi }_2-{\phi }_1}{2}\right)+\cos ({\phi }_1)\cos ({\phi }_2){\sin }^2\left(\frac{{\lambda }_2-{\lambda }_1}{2}\right)}\right)$$

   (4.138)

   where $d$ is the distance between the two points, $r$ is the radius of the sphere (in our case $r=1$), ${\varphi }_1$, ${\varphi }_2$ the latitude of point 1 and latitude of point 2 (in radians) and ${\lambda }_1$, ${\lambda }_2$ longitude of point 1 and longitude of point 2 (in radians), respectively.

5. 5.

   Once all the distances are calculated, the reference sources are sorted by the angular distance (in increasing order) and the data is stored into the output file (defined by the user).

6. 6.

   Steps 2-5 are repeated until all the sources in the external catalogue have been read.

The cross-match has been scientifically verified by two different tests: first, the basic algorithms of the cross-match (angular distances, coordinates transformations, HEALPix library, etc.) were checked by a direct comparison against the counterpart algorithms provided by the Astropy library (www.astropy.org); and second, a direct comparison of the cross-matched sources were compared with the cross-match service provided by the Gaia Archive (Gaia DR1) (https://archives.esac.esa.int/gaia). We only provide details for this second test. For example, in order to perform this scientific verification, the cross-match of the Hipparcos catalogue (J1991.25) vs. the Gaia DR1 catalogue (J2015) (without any epoch propagation, since this feature was not available in the Gaia Archive at that time) was carried out.

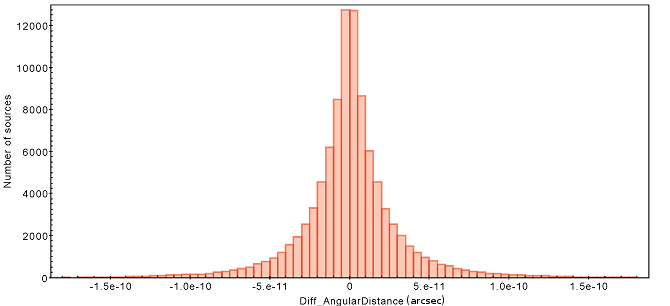
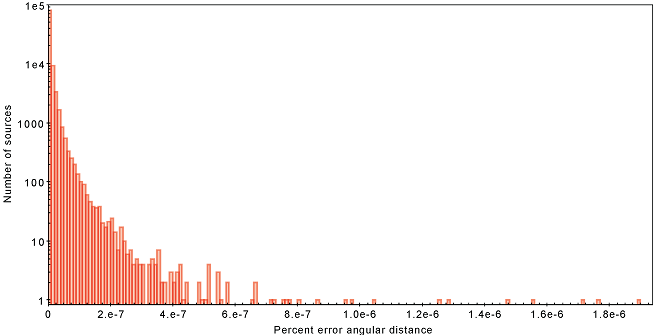
Both algorithms return the same number of cross-matched sources, 95.800. Figure 4.19 displays two histograms: the upper one corresponds to the difference in the calculated angular distance between both algorithms for each cross-matched source, while the other shows the absolute error, i.e., the difference in the angular error between both results. As can be seen, the profile of the histogram presents a very narrow distribution, and the absolute errors are close to the machine precision. The distribution of the relative errors of the differences between the calculated angular distances shows the two methods to provide close to identical results.