4.3.4 Pseudo-colours in source update
Under certain conditions it is possible to derive an approximate estimate of the colour of a source from its astrometric solution (source update), utilizing the chromatic displacements of the image centroids, known as chromaticity. Effectively, the astrometric instrument acts as a spectrometer with extremely low resolution. Astrometric colour information obtained in this way are called pseudo-colours. The necessary conditions for the determination of pseudo-colours are
-
•
that the astrometric instrument has some significant chromaticity – this is in practice always the case for Gaia;
-
•
that the chromaticity was uncorrected in the pre-processing – this is normally not the case for Gaia DR3, where the LSF/PSF calibration is colour dependent (Section 3.3.5), but for sources without a reliable colour (effective wavenumber ) the PSF/LSF for the default colour m was used, which is equivalent to leaving the chromaticity uncorrected in the pre-processing;
-
•
that the chromaticity is adequately calibrated in the AGIS primary solution by means of sources with known colours from the photometric processing, but for which no chromaticity correction was made in the pre-processing.
The last two conditions are mutually exclusive, except if a subset of the sources with known colours are pre-processed in both modes, that is using the default colour as well as the photometrically determined colour. For Gaia DR3 some 25 million sources obtained this special pre-processing. We may call this the chromaticity calibration subset.
As described in Section 4.3.6, the along-scan geometric instrument model includes terms of the form
| (4.103) |
where is the chromaticity parameter (depending on CCD, field of view, time, etc.), is the effective wavenumber (in m) of the source, and m the default value mentioned above. In contrast to Gaia DR2, where was computed from the colour index using an analytical formula, the effective wavenumbers used for the Gaia DR3 astrometry were computed more rigorously as the photon-weighted inverse wavelengths, using the calibrated BP and RP spectra; this was done as part of the BP/RP spectroscopic processing (Section 5.3) at the end of the previous processing cycle (thus corresponding to Gaia DR2 photometry.)
Once the chromaticity in Equation 4.103 has been calibrated as a function of CCD, field of view, time, etc. in a primary solution using the chromaticity calibration subset, it can be used to estimate the pseudo-colour of an arbitrary source by including the corresponding term in the source update model:
| (4.104) |
In this equation is regarded as known (from the previous chromaticity calibration) and is an additional unknown per source, known as the pseudocolour. Because it is solved together with the usual five astrometric parameters, the pseudocolour solution is also referred to as a six-parameter solution. The solution provides an estimate of the full covariance matrix of the estimated parameters, including the standard uncertainty of and its statistical correlation coefficients with the other five parameters.
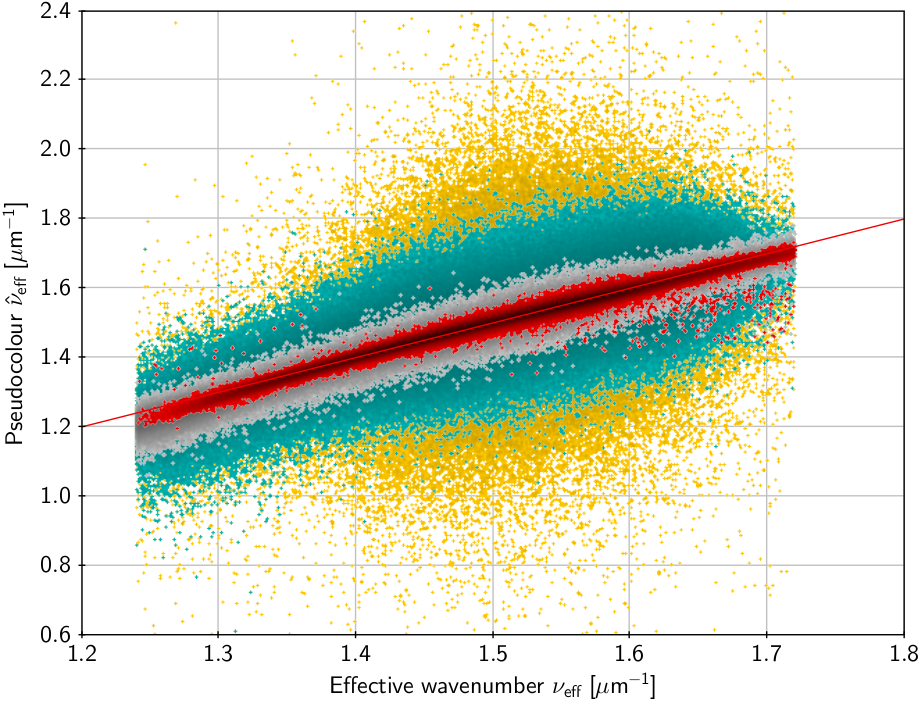
Figure 4.10 shows the relation between and for sources in the chromaticity calibration subset where both quantities are known. The agreement is good when the formal uncertainty of is small. The slight deviation from the 1:1 relation at both ends suggests that the linear model in Equation 4.103 is not fully adequate.
Although there is in Gaia DR3 no longer an exact one-to-one relation between and the colour index , the simple expression
| (4.105) |
provides a reasonably accurate approximation (to within m) for the colour interval . The value of actually used in the astrometric solution is given in the field nu_eff_used_in_astrometry. This field is empty if the default wavenumber was used in pre-processing and astrometry.