2.2.4 Variability
Author(s): Céline Reylé
Regular and semi-regular variables
The Universe Model implements ten types of stellar variability: Cepheid, RRab, RRc, Scuti, roAp, ACV, Semi-regular, Miras, Dor and ZZCeti. The variability probabilities depend on the position in the HR diagram. A summary of the variable type characteristics is given in Table 2.8.
| Type name | Spec. type | Lum. C. | P | Pop. | ||
| Scuti (a) | A0:F2 | III | 0.3 | all | all | — |
| Scuti (b) | A1:F3 | IV:V | 0.3 | all | all | — |
| ACV (a) | B5:B9 | V | 0.016 | thin disc | -1 to 1 | — |
| ACV (b) | A1:A8 | IV:V | 0.01 | thin disc | -1 to 1 | — |
| Cepheid | F5:G0 | I:III | 0.3 | thin disc | -1 to 1 | — |
| RRab | A8:F5 | III | 0.4 | spheroid | -4 to -1 | — |
| RRc | A8:F5 | III | 0.1 | spheroid | -4 to -1 | — |
| RoAp | A0:A9 | V | 0.001 | thin disc | -1 to 1 | — |
| SemiReg (a) | K5:K9 | III | 0.5 | all | all | — |
| SemiReg (b) | M0:M9 | III | 0.9 | all | all | — |
| Miras | M0:M9 | I:III | 1. | all | all | — |
| ZZCeti | White dwarf | — | 1 | all | all | 10800:12300 |
| Dor | F0:F5 | V | 0.3 | all | all | — |
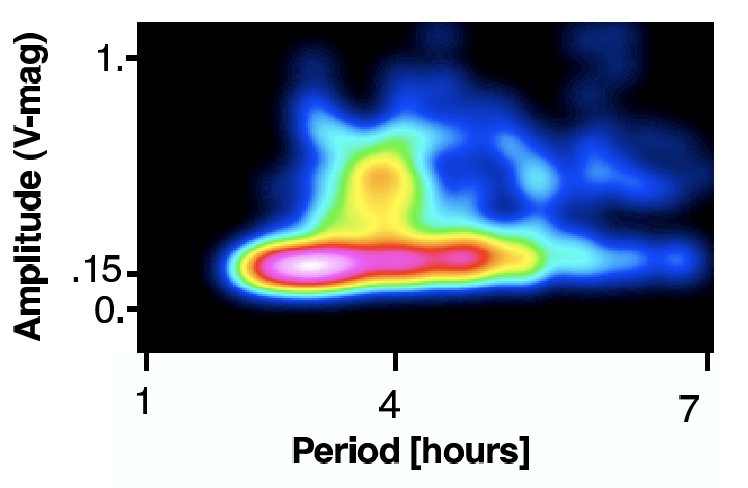
Modelling the amplitude and period distributions by analytic functions may be quite difficult. Period and amplitude are taken randomly from a 2D probability distribution defined for each variability type. We constructed these distributions using existing data (mostly from Hipparcos), and applying some Gaussian smoothing. For example, using the stars from the catalogue of Scuti stars from Rodríguez et al. (2000), the distribution shown in Figure 2.1 is obtained. This method is used for all the variability types except for Dor and ZZCeti (see below).
The light curve of the regular or semi-regular variable stars is defined as follows, with ( is the period, is the phase) :
| Variability type | Light curve |
| Cepheid | |
| Scuti, roAp, RRc, Miras | |
| ACV | , random from 0 to 1 |
| SemiRegular | Inverse Fourier Transform of a Gaussian in frequency space |
The light curves of RR Lyrae variable stars of type RRab are modelled based on six templates from Layden (1998) and seven from Marconi and Clementini (2005). The pulsation periods and amplitudes are chosen from a 2D probability distribution as explained before.
The multi-periodic light curves of Dor variables are simulated using a combination of sine functions. The number of sine functions, their periods and amplitudes are chosen randomly within these ranges, respectively: 3 to 5, 0.3 to 3 days, and 0.005 to 0.025 magnitude.
The light curve model implemented for ZZCeti is based on a semi-numerical model. The model takes periods, amplitudes and phases as input to define a pulsation pattern at the base of the convective zone and solves the problem of flux propagation through the convective zone to derive the relative flux variations at the photosphere. The number of periods, periods, amplitudes, and phase are chosen randomly within these ranges, respectively: 1 to 3, 0.5 to 25 minutes, 0.005 to 0.025 magnitude, and 0 to 1.
For Cepheids, the following period/luminosity relation is considered: (Molinaro et al. 2011) while for Miras, it is (Feast et al. 1989).
The variation of the radius and radial velocity are computed accordingly to the light variation, for stars with radial pulsations (RRab, RRc, Cepheids, Scuti, SemiRegular, and Miras).
Unfortunately, the Hess diagram is empty at the RRLyrae position, therefore RRLyrae will not appear in this GOG version.
Cataclysmic variable stars
Dwarf novae and classical novae are cataclysmic variable stars consisting of close binary star systems in which one of the components is a white dwarf. Half of the white dwarfs are simulated in close binary systems with period 14 hours as dwarf novae. The light curve is simulated by a linear increase followed by an exponential decrease. The time between two bursts, the amplitude, the rising time and the decay time are drawn from Gaussian distributions derived from OGLE observations (Wyrzykowski & Skowron, private communication). The other half of white dwarfs in such systems is simulated as a classical novae.
Microlensing events
Microlensing effects are generated assuming a map of event rate as a function of Galactic coordinates (l,b). The probabilities of lensing over the sky are drawn from the study of Han (2008).
The Einstein crossing time is also a function of the direction of observation in the bulge, obtained from the same paper. The Einstein time of the simulated events are drawn from a Gaussian distribution centred on the mean Einstein time. The impact parameter follows a flat distribution from 0 to 1. The time of maximum is uniformly distributed and completely random, from the beginning to the end of the mission. The Paczynski formula (Paczynski 1986) is used to compute the light curve.
M-dwarfs flares
The statistics for M-dwarf flares are mainly based on Kowalski et al. (2009) and their study on SDSS data: 0.1% of M0-M1 dwarfs, 0.6% of M2-M3 dwarfs, and 5.6% of M4-M6 dwarfs are flaring. Light curve is described as follows:
for for
where is the time of the maximum, is the decay time (in days, random between 1 and 15 minutes), is the baseline magnitude of the source star, is the amplitude in magnitudes (drawn from a Gaussian distribution with and ).
R Coronae Borealis and DY Persei stars
RCrB are carbon stars, however the link with the carbon stars is not fully understood and confirmed. If one assumes the distribution of RCrB and DY Per stars follows this of carbon stars, a rate of ‘outbursting’ carbon stars can be estimated based on the LMC studies. There are around 8000 Carbon stars known in the LMC (e.g. Kontizas et al. (2001)). Soszyński et al. (2009b) based on the OGLE data set the number of candidates for the RCrBs to 23. They also discovered a large number of potential DY Persei stars (around 600). This gives us the rates of 0.003 and 0.075 of carbon stars exhibiting RCrB and DYPer behaviour, respectively.
Apart from their main feature - the dip - they exhibit some small amplitude irregular variability, which can be approximated with two periods:
where, are the periods, are the amplitudes for corresponding periods, is the base magnitude, are the phases of periods. Once the baseline is simulated, the dips can be modelled in three steps: a fading part, the dip where is the amplitude of the dip, and a slow recovery phase (the approximate recovery time is 100 days).
Eclipsing binaries
Eclipsing binaries, while being variables, are treated as binaries and the eclipses are computed from the orbits of the components. See Section 2.2.3.
Stellar rotation
Rotation velocity of stars are computed as a function of spectral type and luminosity class, following Cox and Pilachowski (2000) for supergiants, giants and main sequence, from polynomial fits. For white dwarfs the value of 30 (Kawaler 2003) is used as a typical value. The result is then transformed into by random drawing of the inclination.